Berechnungen zur Funktionalen Sicherheit
Größen, Formeln und Methoden

2 Zuverlässigkeit und verwandte Größen

2.1 Zuverlässigkeit und Unzuverlässigkeit

Zuverlässigkeit \(R(t_1,t_2)\) ist die Wahrscheinlichkeit, dass eine Komponente/ein System/eine Funktion im Zeitintervall \(t_1\) bis \(t_2\) nicht ausfällt, unabhängig davon, ob sie/es zum Zeitpunkt \(t_1\) funktionierte.

Unzuverlässigkeit \(F(t_1,t_2)\) ist die Wahrscheinlichkeit, dass eine Komponente/ein System/eine Funktion im Zeitintervall \(t_1\) bis \(t_2\) ausfällt, unabhängig davon, ob sie/es zum Zeitpunkt \(t_1\) funktionierte. Sie ist folglich die Gegenwahrscheinlichkeit zur Zuverlässigkeit:

\begin{equation} F(t_1,t_2) = 1 - R(t_1,t_2) \quad \textrm {bzw.} \quad R(t_1,t_2) = 1 - F(t_1,t_2) \end{equation}

Bei praktisch allen Fragestellungen wählt man \(t_1=0\) und erhält somit die ein-parametrigen Funktionen \(R(t_1=0,t_2=t)=R(t)\) und \(F(t_1=0,t_2=t)=F(t)\). Für die Beziehung zwischen Zuverlässigkeit und Unzuverlässigkeit gilt entsprechend:

\begin{equation} F(t) = 1 - R(t) \quad \textrm {bzw.} \quad R(t) = 1 - F(t) \end{equation}

Sie wird manchmal auch als Überlebenswahrscheinlichkeit bezeichnet.

Anmerkung: Die Unzuverlässigkeit wird oft auch Ausfallwahrscheinlichkeit genannt. Allerdings wird auch die Nichtverfügbarkeit oft mit Ausfallwahrscheinlichkeit bezeichnet, obwohl sie eine völlig andere Größe ist. Um Missverständnisse zu vermeiden, sollte der Begriff Ausfallwahrscheinlichkeit daher nicht verwendet werden.

Anmerkung: Insbesondere bei Fahrzeugen bezieht man die Zuverlässigkeit und auch die nachfolgenden Größen manchmal auf die zurückgelegte Strecke. Aus \(F(t_1,t_2)\) wird dann \(F(s_1,s_2)\) etc. In allen angegebenen Formeln muss dann die Zeit durch die Strecke ersetzt werden.

Beispiel 2.1 Gefragt sei die Wahrscheinlichkeit \(p\), dass eine Komponente mit dem Alter \(t\) innerhalb der nächsten Stunde ausfällt. Dabei soll nicht vorausgesetzt werden, dass sie zum Zeitpunkt \(t\) noch funktioniert:
\(\seteqnumber{0}{}{2}\)
\begin{equation*} p=F(t,t+1\,\mathrm {h})=F(t+1\,\mathrm {h})-F(t) \end{equation*}

Beispiel 2.2 Gefragt sei die Wahrscheinlichkeit \(p\), dass eine Komponente mit dem Alter \(t\), die zum Zeitpunkt \(t\) noch funktioniert, innerhalb der nächsten Stunde ausfällt:
\(\seteqnumber{0}{}{2}\)
\begin{equation*} p=\frac {F(t,t+1\,\mathrm {h})}{R(t)}=\frac {F(t+1\,\mathrm {h})-F(t)}{R(t)} =\frac {R(t)-R(t+1\,\mathrm {h})}{R(t)} \end{equation*}

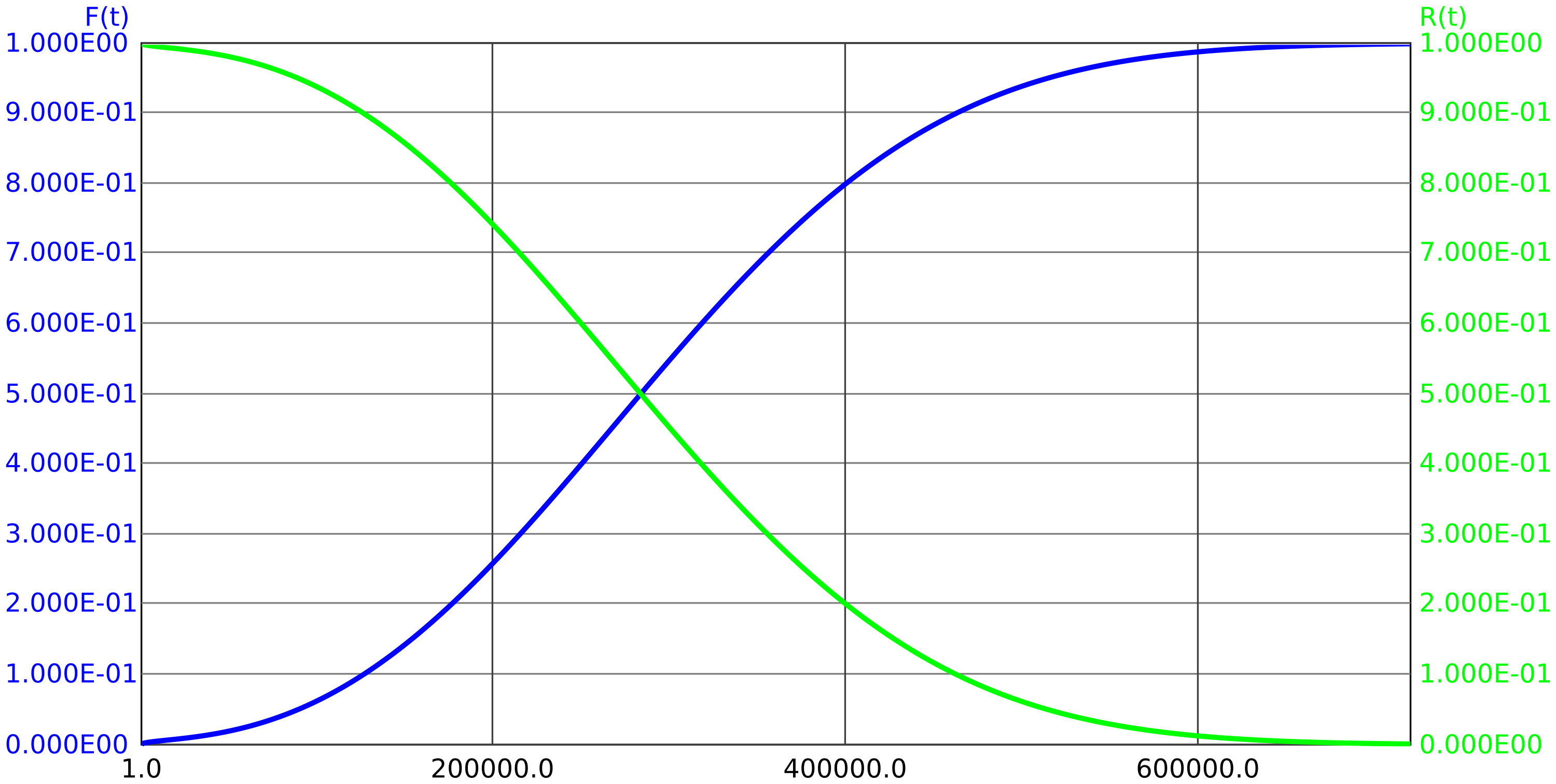
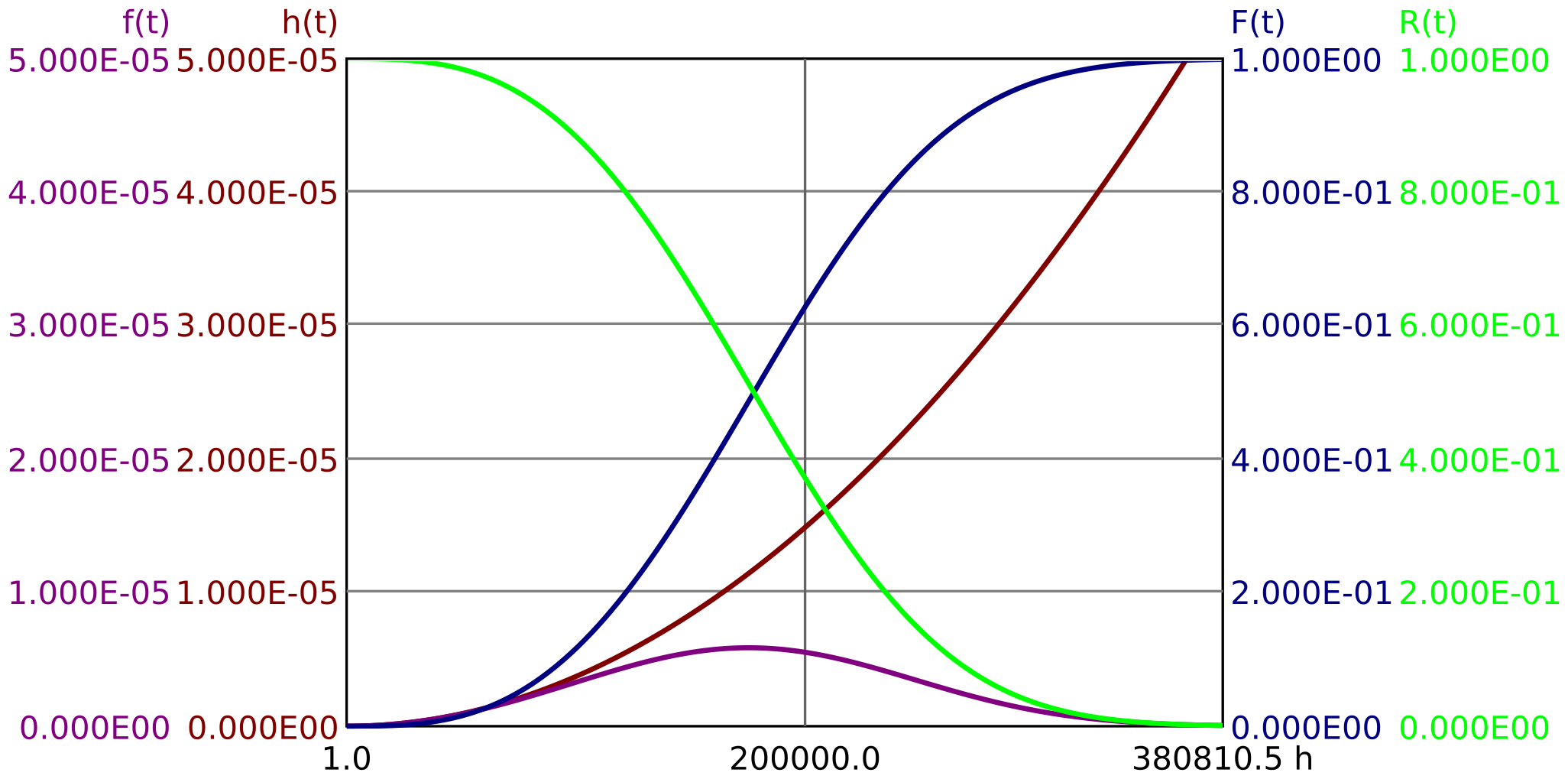
Beispiel 2.3 Aus langjähriger Erfahrung sei bekannt, dass die Zuverlässigkeit bzw. Unzuverlässigkeit den in Abbildung 1 dargestellten (kumulierten) Verteilungsfunktionen folge.

Abbildung 1: Beispielhafte Zuverlässigkeits- und Unzuverlässigkeitsfunktion

Frage 1: Wie groß ist die Wahrscheinlichkeit, dass die Komponent mehr als 40000 Stunden funktioniert?

Antwort: \(p=R(\SI {40000}{\hour }) \approx \num {0,2}\). Folglich wird die Komponente mit 20% Wahrscheinlichkeit länger als 40000 Stunden funktionieren.

Frage 2: Wie groß ist die Wahrscheinlichkeit, dass die Komponente zwischen 40000 und 50000 Betriebsstunden ausfällt?

Antwort: \(p=F(\SI {50000}{\hour })-F(\SI {40000}{\hour })=R(\SI {40000}{\hour })-R(\SI {50000}{\hour })\approx \num {0,15}\). Die Komponente wird also mit 15% Wahrscheinlichkeit nach 40000 bis 50000 Stunden ausfallen.

Frage 3: Wie groß ist die Wahrscheinlichkeit, dass die Komponente zwischen 40000 und 50000 Betriebsstunden ausfällt, wenn sie bei 40000 Stunden noch funktioniert hat?

Antwort: \(p=\dfrac {F(\SI {50000}{\hour })-F(\SI {40000}{\hour })}{R(\SI {40000}{\hour })}\approx \dfrac {\num {0,15}}{\num {0,2}}=\num {0,75}\).

2.2 Ausfalldichte und Ausfallrate

Die Änderung der Unzuverlässigkeit pro Zeit ist die Ausfalldichte. Für beliebige Ausfalldichtefunktionen \(f(t)\) gilt:

\begin{equation} F(t) = \int \limits _0^t f(\tau )\;d\tau \quad \textrm {bzw.} \quad f(t) = \frac {dF(t)}{dt} = -\,\frac {dR(t)}{dt} \end{equation}

Im Gegensatz zur Unzuverlässigkeit ist die Ausfalldichte keine Wahrscheinlichkeit. Sie kann beliebige positive Werte annehmen und hat eine Dimension (meist 1/Zeit oder 1/Strecke).

Da die Unzuverlässigkeit für \(t \rightarrow \infty \) gegen 1 geht, muss für jede Dichtefunktion gelten:

\begin{equation} \int \limits _0^\infty f(\tau )\;d\tau = 1 \end{equation}

Die Ausfallrate \(h(t)\) ist für beliebige Ausfalldichtefunktionen gegeben als

\begin{equation} h(t) = \frac {f(t)}{R(t)} = \frac {f(t)}{1-F(t)} \end{equation}

Mit \(f(t) = -\frac {dR(t)}{dt}\) ergibt sich:

\begin{equation} h(t) = \frac {f(t)}{R(t)} = \frac {-dR(t)/dt}{R(t)} = -\,\frac {\dot {R}}{R} \end{equation}

\begin{equation} R(t) = \mathrm {e}^{-\int \limits _0^t h(\tau )\,d\tau } \end{equation}

\begin{equation} \label {eq:F_h} F(t) = 1-\mathrm {e}^{-\int \limits _0^t h(\tau )\,d\tau } \end{equation}

Eine Ausfallverteilung ist durch \(f(t)\) oder \(F(t)\) oder \(R(t)\) oder \(h(t)\) vollständig beschrieben.

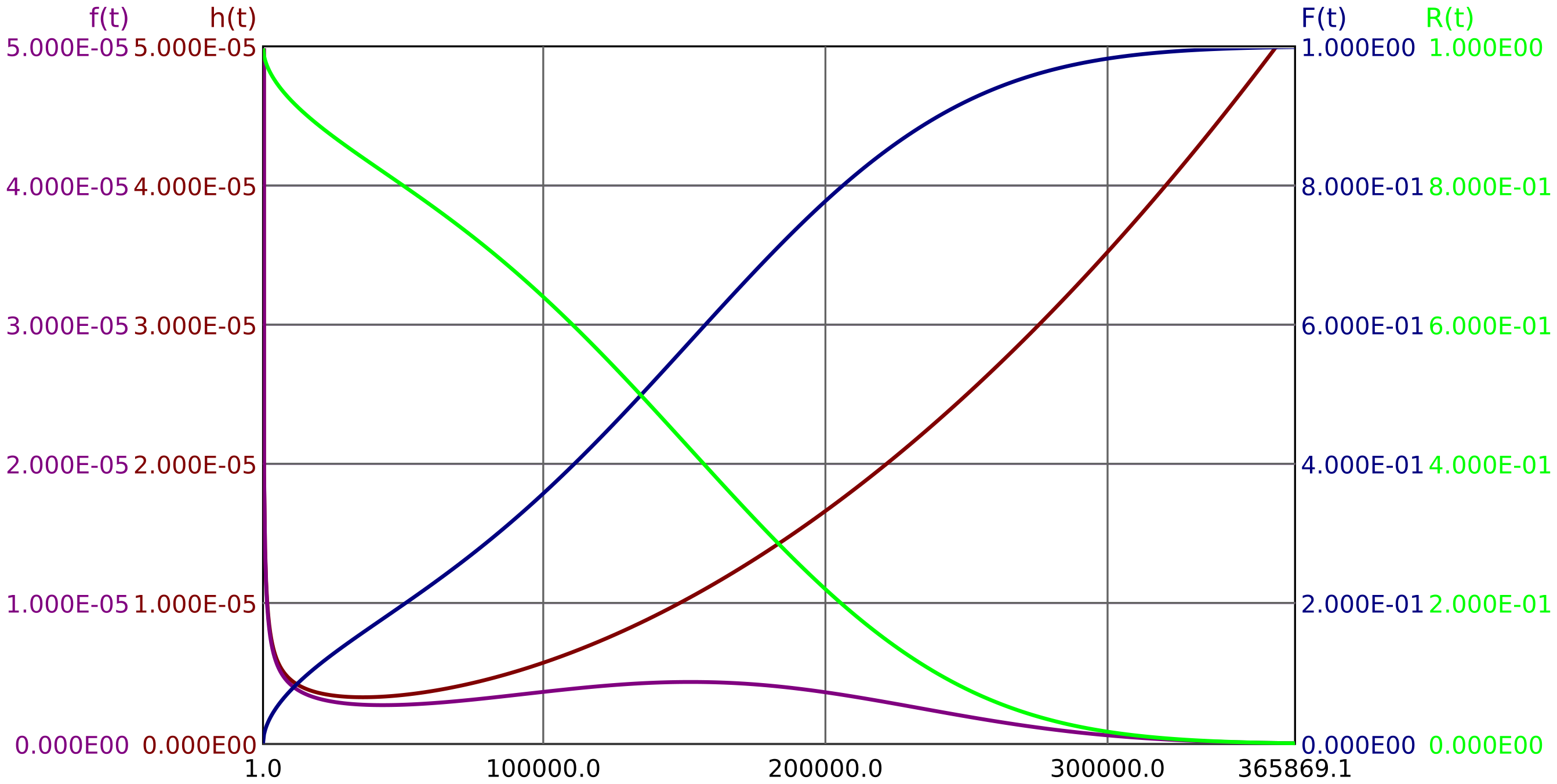
Abbildung 2 zeigt eine beispielhafte Ausfallverteilung und die sie beschreibenden Größen.

Anmerkung: Während die Symbole \(R(t)\), \(F(t)\) und auch \(f(t)\) weitgehend einheitlich verwendet werden, hat sich für die Ausfallrate noch kein Symbol durchgesetzt. Anstelle von \(h(t)\) findet man auch \(\Lambda (t)\) oder \(\lambda (t)\).

Die Ausfallrate \(h(t)\) gibt die Wahrscheinlichkeit eines Ausfalles pro Zeitintervall an, unter der Bedingung, dass die Funktion zu Beginn des Zeitintervalls nicht ausgefallen ist:

\begin{equation} h(t) = \frac {f(t)}{R(t)} = \frac {dF(t)/dt}{R(t)} = \frac {1}{R(t)}\,\lim _{\Delta t \rightarrow 0} \frac {F(t+\Delta t) - F(t)}{\Delta t} \end{equation}

Hierbei muss das Zeitintervall \(\Delta t\) hinreichend klein sein! Daher darf diese Gleichung keinesfalls herangezogen werden, um eine mittlere Ausfallrate über einen längeren Zeitraum zu berechnen. Die hierfür erforderlichen Formeln sind in Abschnitt 3 erwähnt.

2.3 Badewannenkurve

Jedes nicht extrem einfache Bauteil kann auf unterschiedliche Weise ausfallen. Jeder dieser Ausfallmodi hat eine eigene Ausfallverteilungsfunktion. Fast immer gibt es Ausfallmodi mit abnehmender Ausfallrate, diese sind meist auf Produktionsfehler zurückzuführen. Bei mechanischen oder auch stark belasteten elektronischen Bauteilen gibt es auch Ausfallmodi mit steigender Ausfallrate, dies sind insbesondere die auf Verschleiß oder Alterung zurückzuführenden Ausfälle. Die Gesamt-Ausfallrate ergibt sich durch Addition der Einzel-Ausfallraten aller n Fehlermodi:

\begin{equation} h(t) = \sum _{i=1}^n h_i(t) \end{equation}

Sobald es mindestens je einen Ausfallmodus mit fallender und einen mit steigender Ausfallrate gibt, ähnelt der Graph der Gesamt-Ausfallrate \(h(t)\) einer Badewanne, siehe Abbildung 2.

2.4 Mittlere Zeit bis zum Ausfall (MTTF)

Die mittlere Zeit (genauer: Betriebsdauer) bis zum Ausfall (engl.: Mean Time To Failure, kurz MTTF) ist der Erwartungswert der Zeit bis zum Ausfall. Sie berechnet sich für beliebige Ausfallverteilungen wie folgt:

\begin{equation} \label {eq:MTTF} \mathrm {MTTF} = \int \limits _0^\infty t \cdot f(t)\,dt \end{equation}

Dieser Wert wird in Abschnitt 3 als natürliche MTTF bezeichnet, da es der Wert ist, der sich experimentell ergibt, wenn die Komponente immer bis zum Ausfall betrieben wird und dann ersetzt wird. In der Praxis ist dies jedoch oft nicht der Fall, so dass insbesondere zur Bestimmung von mittleren Ausfallraten andere Formeln gelten, siehe Abschnitt 3.

2.5 Verteilungsfunktionen

In diesem Abschnitt werden einige Verteilungsfunktionen vorgestellt, die in der Praxis oder für nachfolgende Betrachtungen relevant sind. Weitere Verteilungen sind in Anhang C beschrieben.

2.5.1 Exponentialverteilung

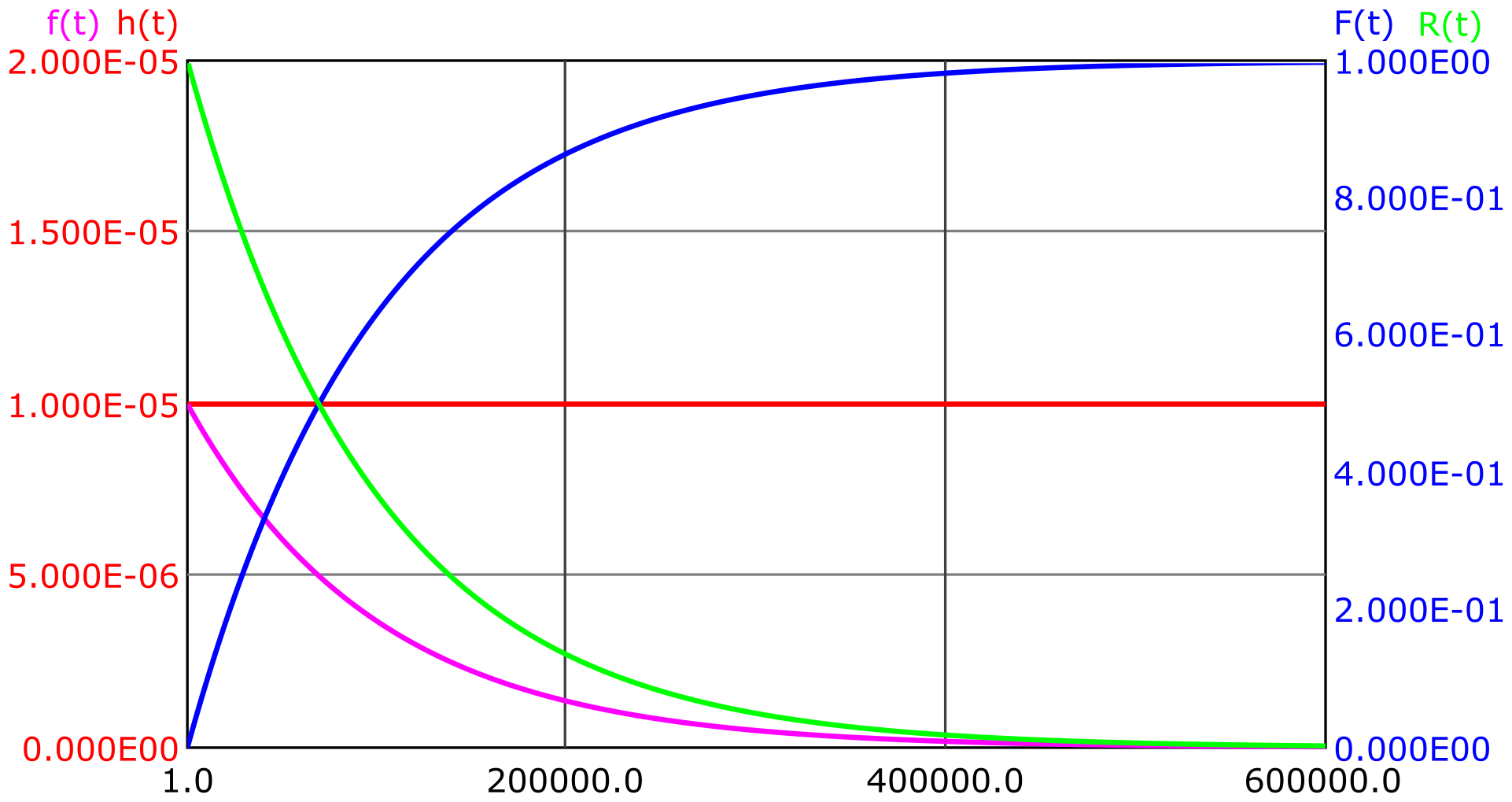
Die Exponentialverteilung zeichnet sich durch eine konstante Ausfallrate \(h(t)=const\) aus. Die Ausfallrate wird also durch einen einzigen Parameter beschrieben, welcher mit \(\lambda \) bezeichnet wird. Die Exponentialverteilung ist die einfachste und zugleich wichtigste Verteilungsfunktion. Sie trifft für gedächtnislose Komponenten zu, also dann, wenn das Alter der Komponente keinen nennenwerten Einfluss auf die Ausfallrate hat (auch als ergodisches Verhalten bezeichnet). Der zeitliche Verlauf von Zuverlässigkeit \(R(t)\), Unzuverlässigkeit \(F(t)\), Ausfallrate \(h(t)\) und Ausfalldichte \(f(t)\) ist in Abbildung 3 dargestellt.

Die Exponential-Verteilung ist durch die folgenden Gleichungen beschrieben:

\begin{equation} f(t)=\lambda \cdot \mathrm {e}^{-\lambda \cdot t} \end{equation}

\begin{equation} F(t) = 1 - \mathrm {e}^{-\lambda \cdot t} \end{equation}

\begin{equation} R(t) = \mathrm {e}^{-\lambda \cdot t} \end{equation}

Die mittlere Zeit bis zum Ausfall ist:

\begin{equation} \mathrm {MTTF} = \int _0^\infty t \cdot \lambda \cdot \mathrm {e}^{-\lambda \cdot t}\,dt = - \frac { \left ( \lambda \cdot t + 1 \right ) \, \mathrm {e}^{-\lambda \cdot t} } {\lambda } \Big |_0^\infty = \frac {1}{\lambda } \end{equation}

Beispiel 2.4 Gefragt ist die Wahrscheinlichkeit \(p\), dass eine Komponente mit dem Alter \(t\), die zum Zeitpunkt \(t\) noch funktioniert, innerhalb der nächsten Stunde ausfällt. Es sei bekannt, dass die Komponente sich durch eine konstante Ausfallrate beschreiben lässt.
\(\seteqnumber{0}{}{15}\)
\begin{align*} p=\frac {F(t,t+1\,\mathrm {h})}{R(t)} &=\frac {F(t+1\,\mathrm {h})-F(t)}{R(t)} = \frac {\mathrm {e}^{-\lambda \cdot t} - \mathrm {e}^{-\lambda \cdot (t+1\,\mathrm {h})}} {\mathrm {e}^{-\lambda \cdot t}} \\ &= \frac {\mathrm {e}^{-\lambda \cdot t} - \mathrm {e}^{-\lambda \cdot t} \cdot \mathrm {e}^{-\lambda \cdot 1\,\mathrm {h}}} {\mathrm {e}^{-\lambda \cdot t}} = 1 - \mathrm {e}^{-\lambda \cdot 1\,\mathrm {h}} \end{align*} Wie zu erwarten war, taucht das Alter der Komponente \(t\) im Ergebnis nicht auf.

Viele Elemente lassen sich durch eine konstante Ausfallrate hinreichend genau beschreiben. Insbesondere kann bei Elementen eines Systems, deren Lebensdauer kürzer ist als die System-Einsatzdauer, und die nicht zu bestimmten Zeitpunkten präventiv getauscht werden, im Rahmen von System-Berechnungen ohnehin nur eine konstante mittlere Ausfallrate \(h(t)=\overline {h}=\lambda \) angegeben werden, da die tatsächliche Ausfallratenfunktion selbst zufällig ist.

2.5.2 Weibull-Verteilung

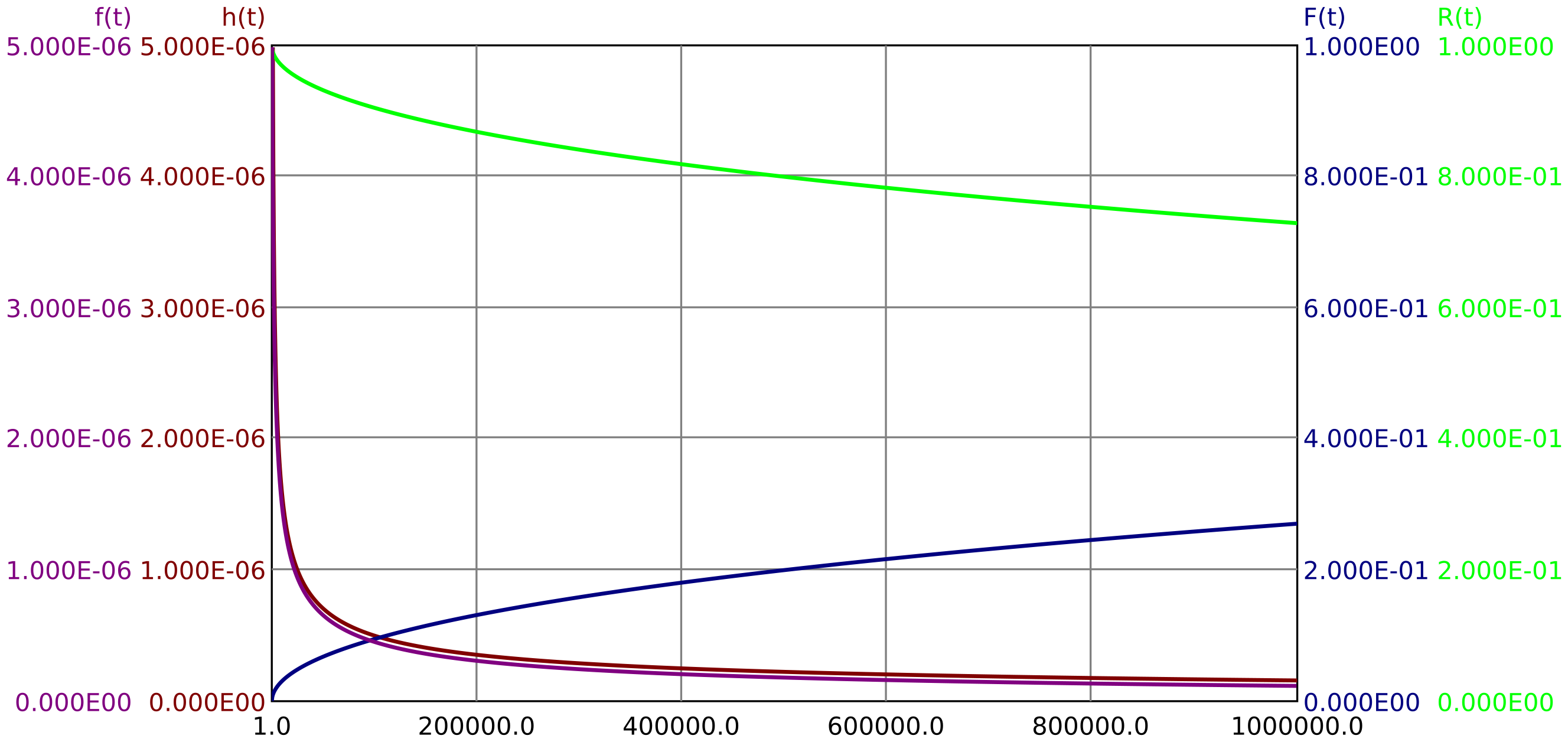
Die Weibull-Verteilung ist eine Verallgemeinerung der Exponentialverteilung. Durch einen zusätzlichen Parameter \(k>0\) im Exponenten können fallende oder steigende Ausfallraten modelliert werden. Für \(0<k<1\) ergibt sich eine fallende, für \(k>1\) eine steigende Ausfallrate. Für \(k=1\) ergibt sich die Exponentialverteilung.

\begin{equation} \label {eq:Weibull_h} h(t) = \lambda \cdot k \cdot (\lambda \cdot t)^{k-1} \end{equation}

\begin{equation} \label {eq:Weibull_f} f(t)=\lambda \cdot k \cdot (\lambda \cdot t)^{k-1} \mathrm {e}^{-(\lambda \cdot t)^k} \end{equation}

\begin{equation} \label {eq:Weibull_F} F(t) = 1 - \mathrm {e}^{-(\lambda \cdot t)^k} \end{equation}

\begin{equation} \mathrm {MTTF} = \frac {1}{\lambda } \cdot \Gamma \left (1+\frac {1}{k}\right ) \end{equation}

Fehlermodi, die ausschließlich auf Abnutzung zurückzuführen sind, können in der Regel für eine bestimmte Zeit \(t_0\) völlig ausgeschlossen werden. Diese Fehlermodi kann man meist gut mit einer Weibull-Verteilung mit \(k>1\) (steigende Ausfallrate) modellieren, die zusätzlich noch um \(t_0>0\) nach rechts verschoben ist:

\begin{equation} h(t) = \lambda \cdot k \cdot (\lambda \cdot (t-t_0))^{k-1} \quad \text {f\"ur}~t>t_0 \end{equation}

Hinweis: Insbesondere im englischsprachigen Raum wird die Weibull-Verteilung oft mit \(\mu =1/\lambda \) parametriert.

Die Abbildungen 4 und 5 und zeigen eine Weibull-Verteilung mit fallender Ausfallrate (k=0,5) und eine mit steigender Ausfallrate (k=3).

2.5.3 Sterblichkeit

Auch die Sterblichkeit des Menschen ist eine Verteilungsfunktion, wenngleich diese nicht direkt einer mathematische Funktion folgt. In Abbildung 6 ist die Querschnittsbetrachtung der Sterblichkeit der westdeutschen Bevölkerung in den Jahren 1960-1962 dargestellt.

Die Querschnittsbetrachtung basiert auf der Statistik der Todesfälle in dem genannten Zeitraum. Sie macht damit insbesondere eine Aussage über das tatsächliche mittlere Sterbealter der Menschen, die in diesem Zeitraum gestorben sind. Die Sterberate \(h(t)\) gibt hier also die Wahrscheinlichkeit an, dass eine Person, die das Alter \(t\) erreicht hatte, innerhalb der Zeitspanne \(\Delta t\) stirbt, dividiert durch diese Zeitspanne \(\Delta t\).

Im Gegensatz zur Querschnittsbetrachtung macht die sogenannte Längsschnittbetrachtung eine Aussage über die Sterbeverteilung der in dem jeweiligen Zeitraum geborenen Menschen. Statistische Längsschnittbetrachtungen können also nur für Geburtsjahrgänge gemacht werden, von denen kein Mensch mehr am Leben ist. Für spätere Jahrgänge stellen sie ganz oder teilweise Prognosen dar. Wäre die Sterblichkeitsverteilung unabhängig vom Jahrgang, wären Querschnitts- und Längsschnittverteilung identisch. Für die Längsschnittbetrachtung sind die Größen unmittelbar anschaulich:

• Die Zuverlässigkeit (Überlebenswahrscheinlichkeit) \(R(t)\) ist die Wahrscheinlichkeit, das Alter \(t\) zu erreichen.
• Die Unzuverlässigkeit (Ausfallwahrscheinlichkeit) \(F(t)\) ist die Wahrscheinlichkeit, vor Erreichen des Alters \(t\) zu sterben.
• Die Ausfalldichte \(f(t)\) ist die Wahrscheinlichkeit, im Alter zwischen \(t\) und \(t+\Delta t\) zu sterben, dividiert durch den Zeitraum \(\Delta t\), mit \(\Delta t \rightarrow 0\).
• Die Ausfallrate \(h(t)\) ist die Wahrscheinlichkeit, im Alter zwischen \(t\) und \(t+\Delta t\) zu sterben, unter der Bedingung, das Alter \(t\) erreicht zu haben, dividiert durch den Zeitraum \(\Delta t\), mit \(\Delta t \rightarrow 0\).
• Die MTTF ist die Lebenserwartung eines Neugeborenen.

Berechnungen zur Funktionalen Sicherheit Größen, Formeln und Methoden