Berechnungen zur Funktionalen Sicherheit
Größen, Formeln und Methoden

3 Mittlere Ausfallrate und mittlere Zeit bis zum Ausfall

Bei vielen Komponenten ist die Ausfallrate stark zeitabhängig. Auch für solche Komponenten wird oft eine mittlere Ausfallrate benötigt, unter anderem aus folgenden Gründen:

• Sollen Systemgrößen ( $\overset{―}{h_{sys}}$ , $\overset{―}{Q_{sys}}$ ) stationär berechnet werden, können prinzipbedingt nur mittlere Ausfallraten verwendet werden.
• Wenn eine Komponente während der Einsatzzeit des Systems wahrscheinlich mehrfach ausfallen (und ersetzt oder repariert werden) wird, ist ab dem ersten Ausfall auch die Ausfallratenfunktion selbst eine Zufallsgröße, die mit zunehmender Anzahl von Ausfällen immer unschärfer wird. Selbst bei transienten, also zeitlich kontinuierlich aufgelösten Betrachtungen, kann also keine Ausfallratenfunktion angegeben werden.
• Falls die Komponente regelmäßig präventiv getauscht werden soll, damit sie möglichst nicht ausfallen wird, stellt sich die Frage, in welchem Intervall die Komponente getauscht werden sollte, um die effektive (Rest-)Ausfallrate und damit die Wahrscheinlichkeit eines Ausfalls möglichst gering zu halten.

In diesem Abschnitt sollen daher die folgenden Aufgaben behandelt werden:

1. Wie groß sind MTTF und mittlere Ausfallrate für den Fall, dass die Komponente bis zum Ausfall betrieben wird und dann getauscht wird? (Beispiel: Glühbirne)
2. Was groß sind MTTF und effektive mittlere Ausfallrate für den Fall, dass die Komponente regelmäßig präventiv getauscht wird? (Beispiel: Steuerriemen eines Verbrennungsmotors)
3. Wenn es gefährliche und ungefährliche Ausfallmodi einer Komponente gibt: Wie können die gefährliche MTTF und die gefährliche mittlere Ausfallrate für die beiden vorgenannten Fälle berechnet werden?

Häufig wird behauptet, man solle bei derlei Fragestellungen die Ausfallrate im flachen Bereich der „Badewannenkurve“ verwenden. Dies ist jedoch nur dann richtig, wenn die Komponente auch wirklich nur in diesem Bereich betrieben wird, also Frühausfälle (insbesondere Produktionsfehler) ebenso absolut ausgeschlossen werden können wie Ausfälle durch Alterung und Verschleiß. Diese Bedingungen sind sehr häufig nicht erfüllt – und zudem weist die Badewannenkurve oft auch gar keinen richtig flachen Bereich auf, sondern sogenannte Frühausfälle überlagern sich mit Spätausfällen.

Anmerkung: Mancher Leser wird sich fragen, warum die Abkürzung MTTF auch für die Zeit zwischen zwei Ausfällen verwendet wird, und nicht etwa MTBF (Mean Time Between Failures). Die Antwort ist einfach, dass fast immer, wenn von MTBF die Rede ist, tatsächlich die MTTF gemeint ist. In Anwendungen oder Berechnungen, in denen Fehlerdetektionszeiten oder Reparaturzeiten nicht unerheblich sind, müssen diese ohnehin ausdrücklich erwähnt werden. Es gibt somit weder in der Sicherheits- noch in der Zuverlässigkeitstheorie einen stichhaltigen Grund, eine Größe MTBF einzuführen oder zu verwenden. ²

² Tatsächlich bin ich nicht sicher, ob ich jemals ein Dokument gesehen habe, in dem der Begriff MTBF korrekt verwendet worden wäre – abgesehen von Lehrbüchern.

3.1 MTTF bei langer Nutzung ohne vorbeugenden Tausch

Zunächst sollen die MTTF und die mittlere Ausfallrate für eine Komponente berechnet werden, welche eine deutlich geringere Lebenserwartung hat als die nominale Einsatzzeit des Gesamtsystems. In dem Fall ist davon auszugehen, dass die Komponente mehrfach ausfallen wird und daher mehrfach getauscht werden muss.

Für beliebige Ausfallverteilungsfunktionen gilt:

$\begin{matrix} (21) & MTTF = \int_{0}^{\infty} t \cdot f (t) d t \end{matrix}$

Liegen ausreichende Test- oder Felddaten vor, so kann dieses Integral leicht mit einer Tabellenkalkulation berechnet werden. Falls anstelle von $f (t)$ die Daten $F (t)$ oder $R (t)$ vorliegen, kann $f (t)$ leicht durch numerisches Differenzieren gewonnen werden.

Ganz allgemein gilt für die Ausfalldichtenfunktion

$\begin{matrix} (22) & f (t) = h (t) \cdot R (t) = h (t) \cdot e^{- \int_{0}^{t} h (τ) d τ} \end{matrix}$

und damit für die MTTF

$\begin{matrix} (23) & MTTF = \int_{0}^{\infty} t \cdot h (t) \cdot e^{- \int_{0}^{t} h (τ) d τ} d t \end{matrix}$

Fast alle Komponenten haben mehrere Fehlermodi, die unterschiedlichen Ausfallverteilungsfunktionen gehorchen. Angenommen die Ausfallverteilungsfunktionen der einzelnen Fehlermodi seien bekannt, wie kann dann die MTTF berechnet werden? Dazu muss vorausgesetzt werden, dass die Fehlermodi voneinander unabhängig sind, also sich nicht gegenseitig beeinflussen. Damit diese Voraussetzung erfüllt ist, ist insbesondere notwendig, dass die Komponente im Fall eines jeden Ausfalls ausgetauscht wird. Dann gilt für die Gesamt-Ausfallratenfunktion $h (t)$ der Komponente, dass sie durch die Summe der Ausfallratenfunktionen der einzelnen Fehlermodi gegeben ist:

$\begin{matrix} (24) & h (t) = \sum_{i = 1}^{n} h_{i} (t) \end{matrix}$

Falls sowohl alle $h_{i} (t)$ als auch die jeweils zugehörigen Zuverlässigkeitsfunktionen $R_{i} (t)$ durch mathematische Formeln gegeben sind, ist es hilfreich, das doppelte Integral zu vereinfachen:

$\begin{array}{r} (25) & \begin{aligned} MTTF & = \int_{0}^{\infty} t \cdot h (t) \cdot e^{- \int_{0}^{t} \sum_{i = 1}^{n} h_{i} (τ) d τ} d t = \int_{0}^{\infty} t \cdot h (t) \cdot e^{- \sum_{i = 1}^{n} \int_{0}^{t} h_{i} (τ) d τ} d t \\ = \int_{0}^{\infty} t \cdot h (t) \cdot \prod_{i = 1}^{n} R_{i} (t) d t \end{aligned} \end{array}$ Die so ermittelte MTTF wird im folgenden vollständige MTTF oder natürliche MTTF genannt, denn es ist die mittlere Zeit bis zum Ausfall, die sich ergibt, wenn die Komponente bis zum Ausfall eingesetzt und dann getauscht wird (wie dies in langlebigen Systemen wie Maschinen, Flugzeugen oder Eisenbahnfahrzeugen für viele Komponenten der Fall ist).

Die mittlere Ausfallrate der Komponente für den Fall, dass die Komponente wahrscheinlich (mehrfach) ausfallen wird und dann jeweils ersetzt wird, ist der Kehrwert der vollständigen MTTF:

$\begin{matrix} (26) & λ = \frac{1}{MTTF} \end{matrix}$

3.2 Vorbeugender Tausch und unvollständige MTTF

Im Falle von vorbeugendem Austausch nach einem Zeitintervall $T$ wird die unvollständige MTTF(T) für die Zeitspanne 0 bis $T$ benötigt, ebenso wenn die natürliche MTTF der Komponente (in der Anwendung) wesentlich größer ist als die Lebenszeit des Systems, in dem sie eingesetzt wird. Aus Überlegungen, welche hier nicht wiedergegeben werden können, folgt:

$\begin{matrix} (27) & MTTF (T) = \frac{\int_{0}^{T} t \cdot f (t) d t + T \cdot R (T)}{F (T)} \end{matrix}$

Mit $R (T) = 1 - F (T)$ und den bereits bekannten Formeln für die Beziehung zwischen Zuverlässigkeit und Ausfallrate erhält man eine Formel zur Berechnung von $MTTF (T)$ bei gegebener oder experimentell ermittelter Ausfallratenfunktion $h (t)$ :

$\begin{array}{r} (28) & \begin{aligned} MTTF (T) & = \frac{\int_{0}^{T} t \cdot f (t) d t + T \cdot (1 - F (T))}{F (T)} = \frac{\int_{0}^{T} t \cdot f (t) d t + T}{F (T)} - T \\ = \frac{\int_{0}^{T} t \cdot h (t) \cdot e^{- \int_{0}^{t} h (τ) d τ} d t + T}{1 - e^{- \int_{0}^{T} h (t) d t}} - T \end{aligned} \end{array}$ Für $T \to \infty$ geht die unvollständige MTTF(T) in die vollständige MTTF über.

Der Kehrwert der unvollständigen MTTF zur Zeit $T$ ist die effektive Ausfallrate $λ_{eff}$ . Sie gibt ganz praktisch an, wie oft die Komponente trotz regelmäßiger präventiver Tauschs bei einer (sehr langen) Einsatzzeit des Gesamtsystems $T_{Life, sys}$ ausfallen würde:

$\begin{matrix} (29) & λ_{eff} (T) = \frac{1}{MTTF (T)} = \frac{N (T_{Life, sys})}{T_{Life, sys}} \end{matrix}$

Dabei meint $N (T_{Life, sys})$ die zählbaren Ausfälle der Komponente im System. Man kann MTTF(T) daher auch als die effektive MTTF für ein bestimmtes Tauschintervall $T$ bezeichnen.

Beispiel 3.1 Die Ausfallrate des Steuerriemens eines Motors eines PKW lasse sich durch zwei überlagerte Weibull-Verteilungen beschreiben:

$λ_{1} = 1 \times 10^{- 9} / h; k_{1} = 0, 3 \Rightarrow h_{1} (t) = 1 \times 10^{- 9} / h \cdot 0, 3 \cdot (1 \times 10^{- 9} / h \cdot t)^{0, 3 - 1}$

$λ_{2} = 2 \times 10^{- 4} / h; k_{2} = 4, 0 \Rightarrow h_{2} (t) = 2 \times 10^{- 4} / h \cdot 4, 0 \cdot (2 \times 10^{- 4} / h \cdot t)^{4, 0 - 1}$

Dabei beschreibt $h_{1} (t)$ sogenannte Frühausfälle, wie sie etwa durch fehlerhafte Komponenten oder fehlerhafte Montage entstehen, und $h_{2} (t)$ die verschleißbedingten Ausfälle des Riemens.

Für die Ausfallrate des Steuerriemens gilt gemäß Formel (24):

$h_{ges} (t) = h_{1} (t) + h_{2} (t)$

Weiter sei angenommen, dass ein PKW mindestens 5000 Betriebsstunden wirtschaftlich betrieben werden können soll.

Mit dieser Ausfallratenfunktion errechnet sich die Unzuverlässigkeit zum Zeitpunkt $T = 5000 h$ zu $F (5000 h) \approx 0, 64$ . Es wäre also bei mindestens jedem zweiten Fahrzeug zu erwarten, dass der Steuerriemens reißt, bevor 5000 Betriebsstunden erreicht sind. Da der Riss des Steuerriemens eines Motors meist einen Totalschaden des Motors und somit oft einen wirtschaftlichen Totalschaden des Fahrzeugs mit sich bringt, stellt sich die Frage, ob nicht ein präventiver Tausch nach einer bestimmten Zeit (oder Fahrstrecke) sinnvoll ist.

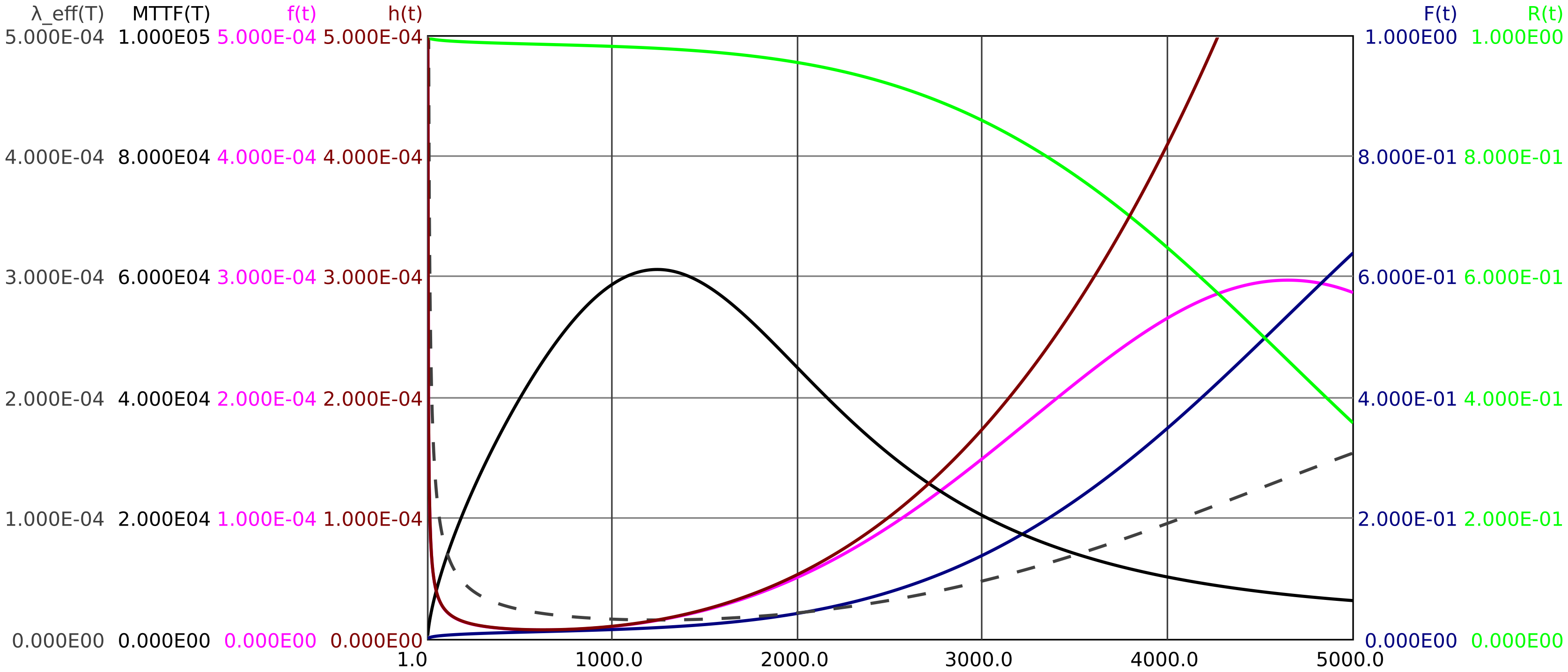
In Abbildung 7 sind neben Ausfalldichte $f (t)$ , Ausfallrate $h (t)$ , Zuverlässigkeit $R (t)$ und Unzuverlässigkeit $F (t)$ auch die effektive $MTTF (T)$ und (gestrichelt) die effektive Ausfallrate $λ_{eff} (T)$ in Abhängigkeit der Zeit bis zum präventiven Tausch $T$ dargestellt.

Abbildung 7: Zuverlässigkeit eines Steuerriemens

Man erkennt, dass bei einer Einsatzzeit $T$ von etwa 1200 Stunden die MTTF(T) mit etwa 61000 h ein Maximum annimmt. Wechselt man also nach etwa 1200 Stunden den Steuerriemen, beträgt die effektive Ausfallrate $λ_{eff} \approx 1, 6 \times 10^{- 5} / h$ . Wird der Riemen häufiger gewechselt, sinkt die effektive (unvollständige) MTTF(T), da Frühausfälle noch einen relativ starken Einfluss haben. Wird der Riemen länger betrieben, sinkt die effektive MTTF(T) ebenfalls, da sich Ausfälle aufgrund von Verschleiß stärker bemerkbar machen. Der präventive Tausch sollte also nach etwa 1200 Stunden (oder einer entsprechenden Strecke) vorgeschrieben werden.

Die effektive MTTF(T) von 61000 h bedeutet bei einem Tauschintervall von 1200 h praktisch, dass etwa jeder fünfzigste (61000 h/1200 h $\approx$ 50) Riemen im Betrieb reißen wird. ³

³ Die Ausfallratenfunktionen sind natürlich erfunden und statistische Unsicherheiten wie Umweltbedingungen, Straßenarten, Fahrstil etc. außer Acht gelassen.

3.3 Gefährliche und ungefährliche Ausfallmodi, gefährliche MTTF

Viele insbesondere komplexere Komponenten können verschiedenartig ausfallen. Dabei sind oft einige Ausfallarten sicherheitskritisch, andere nicht. Für Sicherheitsbetrachtungen ist es daher oft sinnvoll oder erforderlich, zwischen gefährlichen (dangerous, d) und ungefährlichen (safe, s) Ausfallarten zu unterscheiden. Die Gesamt-Ausfallrate zu jeder Zeit t ist die Summe zweier Teil-Ausfallraten für gefährliche und ungefährliche Ausfälle:

$\begin{matrix} (30) & h (t) = h_{d} (t) + h_{s} (t) \end{matrix}$

Die Dichte kann man über

$\begin{array}{r} (31) & \begin{aligned} f (t) & = h (t) \cdot R (t) = (h_{d} (t) + h_{s} (t)) \cdot R (t) \\ = h_{d} (t) \cdot R (t) + h_{s} (t) \cdot R (t) \\ = φ_{d} (t) + φ_{s} (t) \end{aligned} \end{array}$ in zwei Teil-Ausfalldichten $φ_{d}$ und $φ_{s}$ zerlegen ( $φ_{d}$ und $φ_{s}$ sind selbst keine Dichten, da ihre einzelnen Integrale kleiner 1 sind).

Entsprechend kann man die Verteilungsfunktion $F (t)$ in zwei Teilfunktionen zerlegen:

$\begin{matrix} (32) & F (t) = Φ_{d} (t) + Φ_{s} (t) = \int_{0}^{t} φ_{d} (τ) d τ + \int_{0}^{t} φ_{s} (τ) d τ \end{matrix}$

Aus ähnlichen Überlegungen wie für die unvollständige $MTTF (T)$ erhält man für die effektive gefährliche ${MTTF}_{d} (T)$ :

$\begin{matrix} (33) & {MTTF}_{d} (T) = \frac{\int_{0}^{T} t \cdot f (t) d t + T \cdot R (T)}{Φ_{d} (T)} \end{matrix}$

Mit den bereits bekannten Formeln für die Beziehung zwischen Zuverlässigkeit und Ausfallrate erhält man eine Formel zur Berechnung von ${MTTF}_{d} (T)$ bei gegebenen oder experimentell ermittelten Ausfallratenfunktionen $h (t)$ und $h_{d} (t)$ :

$\begin{array}{r} (34) & \begin{aligned} {MTTF}_{d} (T) & = \frac{\int_{0}^{T} t \cdot f (t) d t + T \cdot R (T)}{\int_{0}^{T} φ_{d} (t) d t} = \frac{\int_{0}^{T} t \cdot h (t) \cdot R (t) d t + T \cdot R (T)}{\int_{0}^{T} h_{d} (t) \cdot R (t) d t} \\ = \frac{\int_{0}^{T} t \cdot h (t) \cdot e^{- \int_{0}^{t} h (τ) d τ} d t + T \cdot e^{- \int_{0}^{T} h (t) d t}}{\int_{0}^{T} h_{d} (t) \cdot e^{- \int_{0}^{t} h (τ) d τ} d t} \end{aligned} \end{array}$ Ein einfacher Formelvergleich liefert ferner die Beziehung:

$\begin{matrix} (35) & {MTTF}_{d} (T) = MTTF (T) \frac{F (T)}{Φ_{d} (T)} \end{matrix}$

Auch hier kann man die effektive mittlere gefährliche Ausfallrate $λ_{d}$ als Kehrwert berechnen:

$\begin{matrix} (36) & λ_{d} (T) = \frac{1}{{MTTF}_{d} (T)} \end{matrix}$

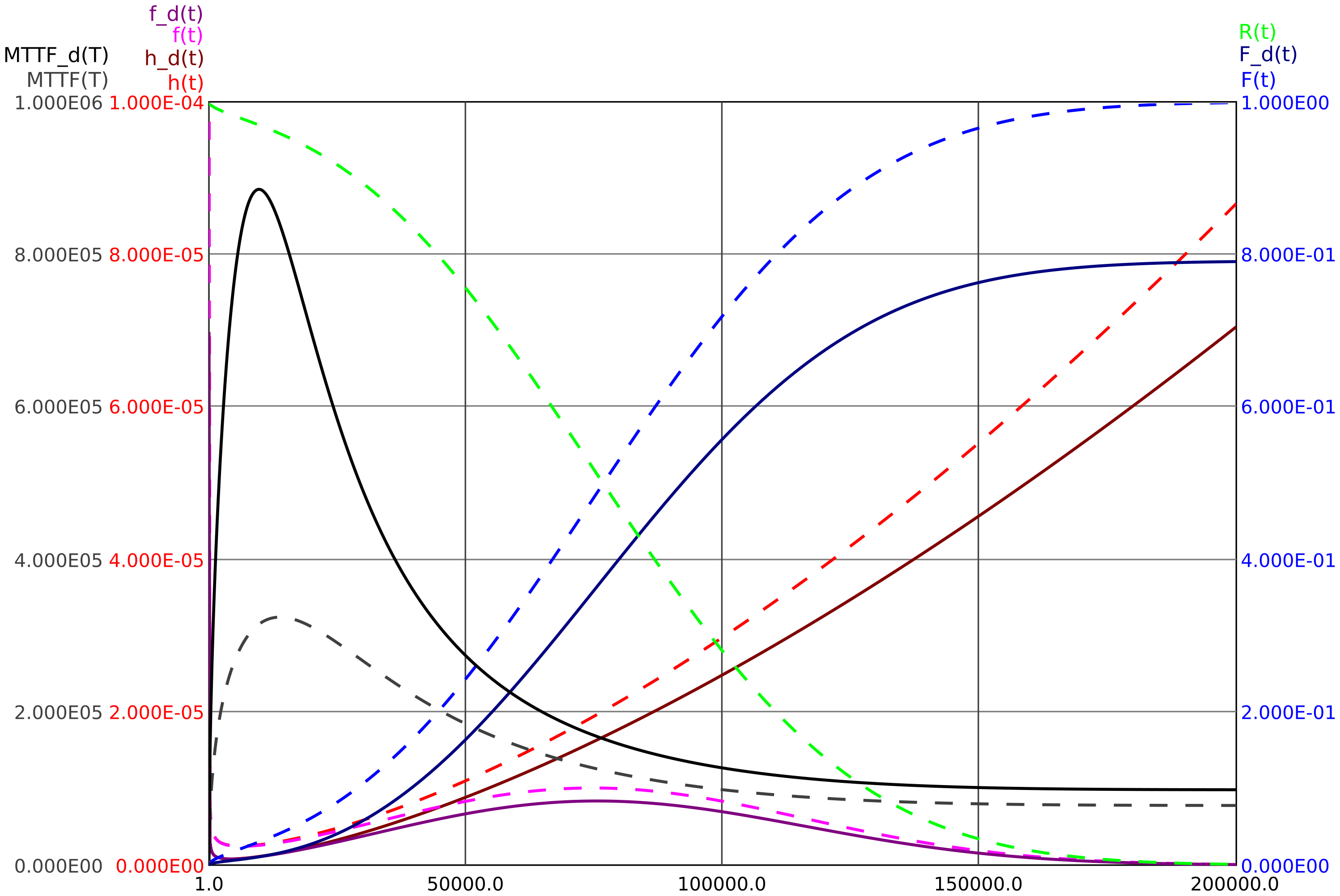
In der folgenden Abbildung 8 sind die für eine Komponente mit je drei gefährlichen und drei ungefährlichen Ausfallarten relevanten Zuverlässigkeitsgrößen dargestellt (durchgezogene Linien für gefährliche Ausfälle, gestrichelte Linien für gesamte Ausfälle):

Berechnungen zur Funktionalen Sicherheit Größen, Formeln und Methoden

3 Mittlere Ausfallrate und mittlere Zeit bis zum Ausfall

3.1 MTTF bei langer Nutzung ohne vorbeugenden Tausch

3.2 Vorbeugender Tausch und unvollständige MTTF

3.3 Gefährliche und ungefährliche Ausfallmodi, gefährliche MTTF

Berechnungen zur Funktionalen Sicherheit
Größen, Formeln und Methoden