Berechnungen zur Funktionalen Sicherheit
Größen, Formeln und Methoden

7 Unzuverlässigkeit von komplexen Funktionen

Die Unzuverlässigkeit ist die wesentliche Größe für Sicherheitsfunktionen, die über eine ganz bestimmte Zeit hinweg funktionieren sollen, und die während dieser Zeit nicht oder nur in begrenztem Umfang gewartet und instandgesetzt werden können.

Nur wenige Systeme und deren Sicherheitsfunktionen fallen in diese Kategorie, etwa bemannte Raumfahrtmissionen. Hier ist nicht die Häufigkeit von Ausfällen, also Unfälle pro Stunde oder Unfälle pro Kilometer gefragt, sondern die Wahrscheinlichkeit, dass die Mission erfolgreich ist, also alle RaumfahrerInnen wieder gesund zur Erde zurückkehren (daher auch der gelegentlich verwendete Begriff „Mission Time“ anstelle von System-Lebenszeit oder Einsatzzeit). Die Mission ist fest vorgegeben, ein einfaches Erreichen eines sicheren Zustands ist nicht möglich (auch wenn es für gewisse Notfälle Abbruch-Szenarien geben mag). Abnutzungsbedingte Ausfälle während der Mission sind nicht anzunehmen. Alle Komponenten werden vor jeder Mission intensiv überprüft, so dass sie wie neu sind. Ab dem Start können die meisten sicherheitsrelevanten Komponenten nicht repariert werden. Das heißt nicht, dass es keine Diagnose geben kann, diese dient dann allerdings nur dazu, eine Komponente abzuschalten, um weiteren Schaden zu verhindern (sofern dies möglich ist) oder um auf eine Ersatz-Komponente umzuschalten (sofern vorhanden).

Da nur wenige Sicherheitsingenieure jemals die Unzuverlässigkeit solcher Systeme berechnen müssen, ist dieses Kapitel recht kurz gehalten.

Selbstverständlich ist die Unzuverlässigkeit nicht nur im Rahmen der Sicherheit relevant (dort wie gesagt eher selten). Auch die Frage „Wie wahrscheinlich ist, dass ein neues Auto innerhalb der ersten 5 Jahre unplanmäßig in die Werkstatt muss?“ ist eine Frage nach der Unzuverlässigkeit. Sie lässt sich allerdings leicht ohne Fehlerbäume oder Markov-Modelle beantworten, da es üblicherweise keine Redundanzen gibt, und daher direkt die Formeln (24) und (8) angewandt werden können, also

\begin{equation} F(T) = 1-\mathrm {e}^{-\int \limits _0^T \sum \limits _{i=1}^n h_i(t)\,dt} = 1-\mathrm {e}^{-\sum \limits _{i=1}^n \int \limits _0^T h_i(t)\,dt} = 1-\prod \limits _{i=1}^n \mathrm {e}^{-\int \limits _0^T h_i(t)\,dt} \end{equation}

Diese Formel kann selbst im Falle komplizierter zeitabhängiger Ausfallraten \(h_i(t)\) leicht mithilfe einer Tabellenkalkulation berechnet werden.

7.1 Berechnung mit Fehlerbäumen

Fehlerbäume können gut zur Berechnung der Unzuverlässigkeit komplexer Systeme verwendet werden. Dabei gibt es zwei Möglichkeiten der Berechnung:

1. Direkt über die Unzuverlässigkeiten \(F(T)\) der Basis-Ereignisse, mit denselben mathematischen Methoden für die Nichtverfügbarkeit in Abschnitt 5 gezeigt. Bei Berechnung über Minimalschnitte wird also zunächst die Unzuverlässigkeit jedes Minimalschnitts berechnet gemäß
\(\seteqnumber{0}{}{71}\)
\begin{equation} F_{\mathrm {MCS}}(T)=\prod \limits _{i=1}^m F_i(T) \label {eq:F_MCS} \end{equation}

und anschließend die System-Unzuverlässigkeit mittels der Formel von Esary-Proschan:
\(\seteqnumber{0}{}{72}\)
\begin{equation} F_{\mathrm {sys}}(T) \lessapprox 1-\prod \limits _{j=1}^n \left ( 1-F_{\mathrm {MCS},i}(T) \right ) \label {eq:F_sys_esary_proschan} \end{equation}

Noch schneller und genauer ist die Verwendung von BDDs.

Diese Methode ist sehr schnell, funktioniert aber nur, wenn keine Verknüpfungen mit Nichtverfügbarkeiten oder sonstigen Wahrscheinlichkeiten, die keine Unzuverlässigkeiten sind (wie etwa die Wahrscheinlichkeit, dass eine externe Randbedingung erfüllt ist), stattfinden. Insbesondere darf der Fehlerbaum also keine Bedingungen oder INHIBIT-Gatter enthalten. Sobald ein Basis-Ereignis eine Nichtverfügbarkeit oder sonstige Bedingung beschreibt, wird diese Methode zu optimistische Ergebnisse liefern ²³.
2. Über die im vorherigen Abschnitt 6 gezeigte Berechnung der Ausfallrate \(h(t)\) (transiente Berechnung) und Anwenden der Formel (8).
\(\seteqnumber{0}{}{73}\)
\begin{equation*} F_\mathrm {sys}(T) = 1-\mathrm {e}^{-\int \limits _0^T h_\mathrm {sys}(t)\,dt} \end{equation*}

Die Methode ist wesentlich langsamer, da die Berechnung der Ausfallrate \(h(t)\) schon aufwändiger ist, und diese auch noch für viele Zeitpunkte erfolgen muss. Sie liefert jedoch auch dann korrekte Ergebnisse, wenn der Fehlerbaum Basis-Ereignisse enthält, die Nichtverfügbarkeiten oder sonstige Bedingungen beschreiben. Dies sollte zwar bei Sicherheitsfunktionen, für die wirklich die Unzuverlässigkeit relevant ist, die Ausnahme sein, kann aber gelegentlich vorkommen.

²³ Ein gutes Tool wird den Benutzer entsprechend warnen oder automatisch auf einen anderen Algorithmus wechseln.

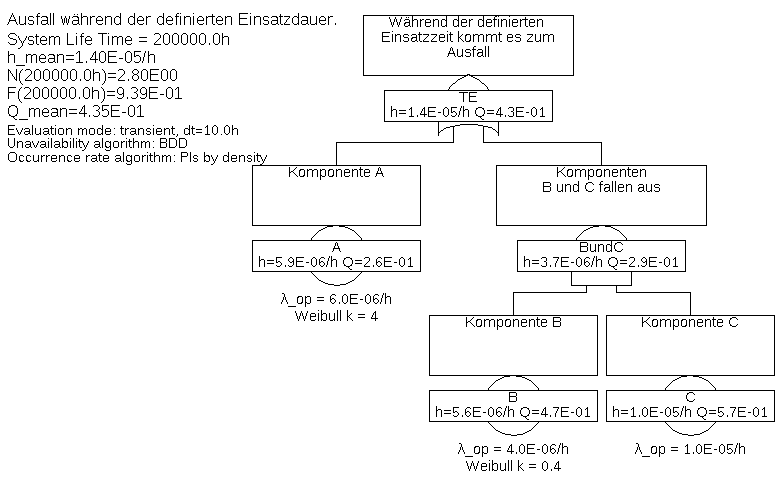
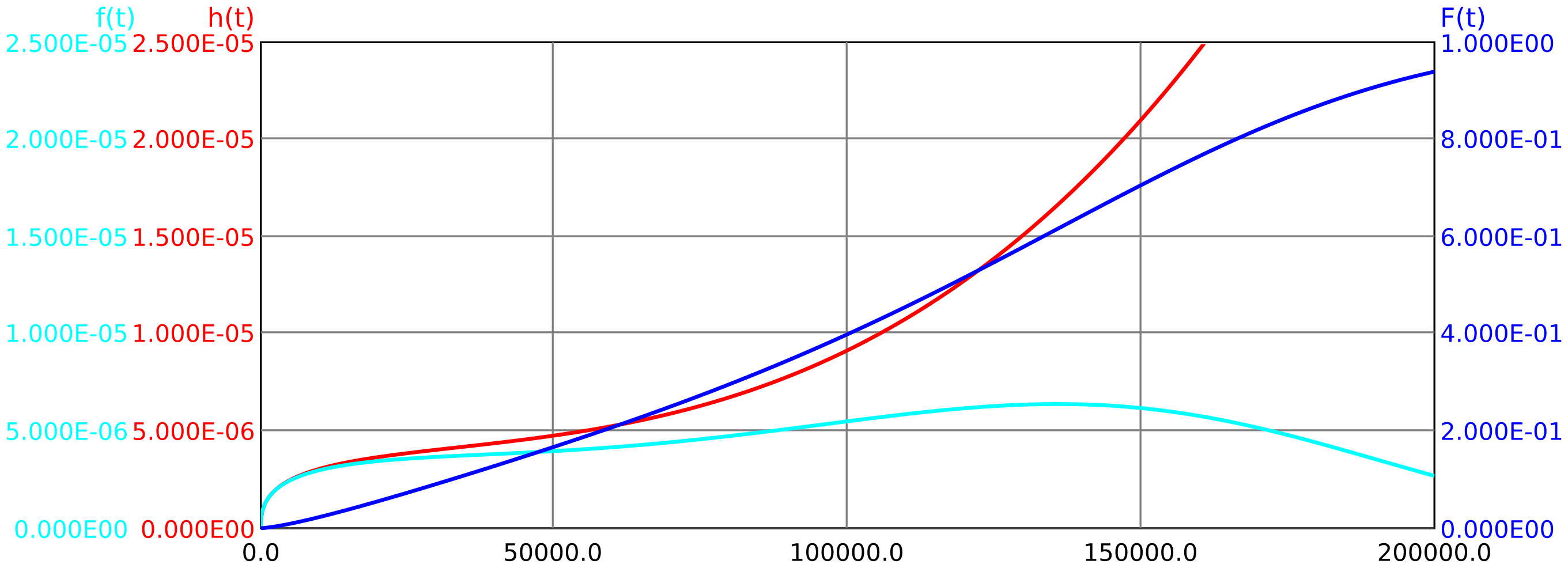
Beispiel 7.1 Für den in Abbildung 37 gezeigten Fehlerbaum soll die Unzuverlässigkeit zum Zeitpunkt \(T=\SI {200000}{\hour }\) mit beiden vorgestellten Methoden berechnet werden.

Abbildung 37: Berechnung der Unzuverlässigkeit mittels Fehlerbaum

Die Unzuverlässigkeit der Basis-Ereignisse A und B wird hier durch Weibull-Verteilungen beschrieben, wobei für A eine zunehmende Ausfallrate (Weibull-Exponent > 1) und für B eine abnehmende Ausfallrate zutreffe (Weibull-Exponent < 1).

Methode 1:

Die Unzuverlässigkeit des Basis-Ereignisses A ergibt sich zu:
\(\seteqnumber{0}{}{73}\)
\begin{equation*} F_\mathrm {A}(T) = 1 - \mathrm {e}^{-(\lambda \cdot T)^k} = 1 - \mathrm {e}^{-(\SI {6.0E-6}{\per \hour } \cdot \SI {200000}{\hour })^{\num {4.0}}} \approx \num {0.874} \end{equation*}

Für Basis-Ereignis B ergibt sich
\(\seteqnumber{0}{}{73}\)
\begin{equation*} F_\mathrm {B}(T) = 1 - \mathrm {e}^{-(\SI {4.0E-6}{\per \hour } \cdot \SI {200000}{\hour })^{\num {0.4}}} \approx \num {0.599} \end{equation*}

und für Basis-Ereignis C gilt
\(\seteqnumber{0}{}{73}\)
\begin{equation*} F_\mathrm {C}(T) = 1 - \mathrm {e}^{-\SI {1.0E-5}{\per \hour } \cdot \SI {200000}{\hour }} \approx \num {0.865} \end{equation*}

Die Minimalschnitte sind {A} und {B&C}, für die System-Unzuverlässigkeit ergibt sich gemäß Formel (73)
\(\seteqnumber{0}{}{73}\)
\begin{equation*} F_\mathrm {sys}(T) \lessapprox 1-\left ( 1-F_\mathrm {A}(T) \right )\cdot \left ( 1-F_\mathrm {B}(T)\cdot F_\mathrm {C}(T) \right ) \approx 1-\left ( 1-\num {0.874} \right )\cdot \left ( 1-\num {0.599}\cdot \num {0.865} \right ) = \num {0.939} \end{equation*}

Moderne Werkzeuge werden BDDs verwenden, damit ergibt sich die System-Unzuverlässigkeit zu
\(\seteqnumber{0}{}{73}\)
\begin{equation*} F_\mathrm {sys}(T) = F_\mathrm {A}(T) + \left ( 1-F_\mathrm {A}(T)\right )\cdot \left ( F_\mathrm {B}(T) \cdot F_\mathrm {C}(T) \right ) \approx \num {0.874} + \left ( 1-\num {0.874} \right )\cdot \left ( \num {0.599}\cdot \num {0.865} \right ) = \num {0.939} \end{equation*}

Dabei wurde die Variablen-Reihenfolge A, B, C gewählt, jede andere Reihenfolge liefert dasselbe Ergebnis.

Methode 2:

Die Ausfallraten der Basis-Ereignisse A und B sind mit Formel (16) gegeben, die Nichtverfügbarkeiten \(Q(t)\) durch Formel (18). Die System-Ausfallrate \(h(t)\) kann nun mit Formel (64) berechnet werden. Die Unzuverlässigkeit wird damit zu \(F_\mathrm {sys}(T)\approx \num {0.964}\) berechnet. Dies ist etwas zu groß, da die Nichtverfügbarkeiten hier sehr groß sind (das System also praktisch nicht verwendbar ist). Wendet man stattdessen die Formel (78) aus Anhang B.1 an, so ergibt sich das korrekte Ergebnis \(F_\mathrm {sys}(T)\approx \num {0.939}\). Der Zeitverlauf von Ausfalldichte \(f(t)\), Ausfallrate \(h(t)\) und Unzuverlässigkeit \(F(t)\) ist in Abbildung 38 gezeigt.

Abbildung 38: Zeitlicher Verlauf von Ausfallrate, Ausfalldichte und Unzuverlässigkeit für Beispiel 7.1

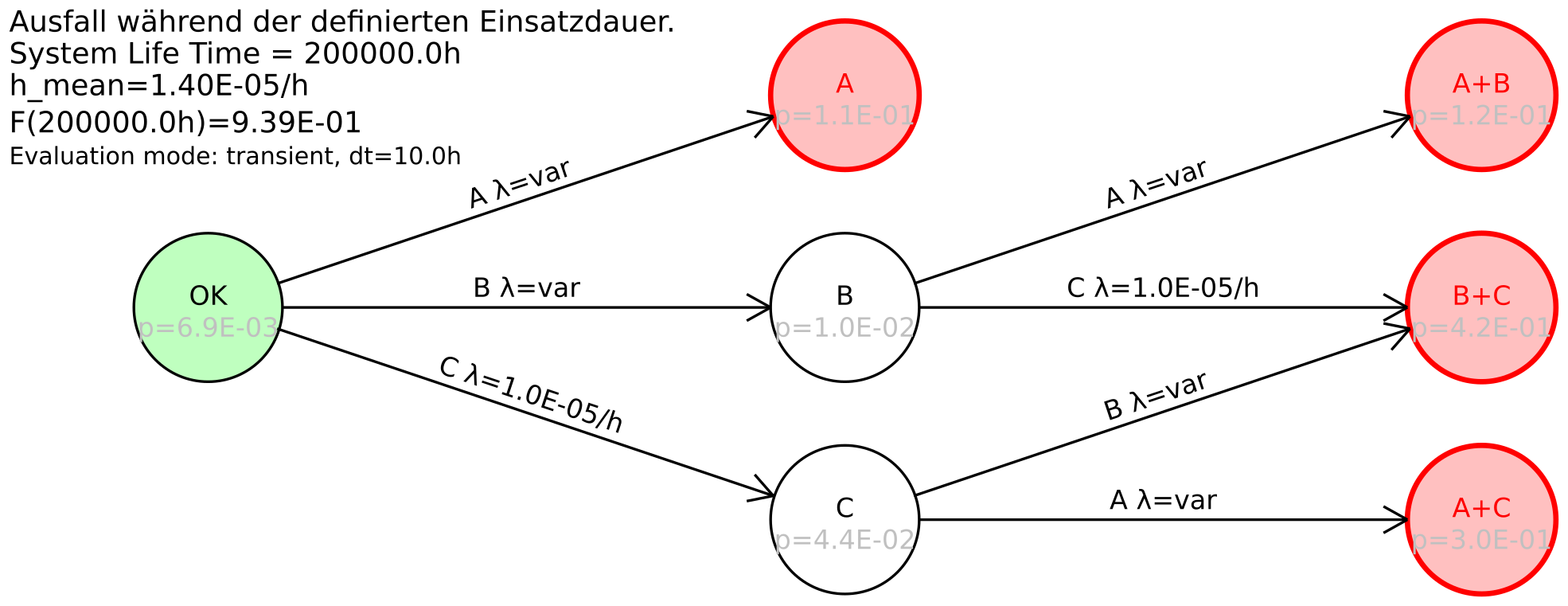
7.2 Berechnung mit Markov Modellen

Die System-Unzuverlässigkeit kann auch mittels Markov-Modellen berechnet werden. Die Berechnung muss nun grundsätzlich durch Integration des Differenzialgleichungssystems erfolgen (transiente Berechnung), da ja nie ein stationärer Zustand angenommen wird. Die System-Unzuverlässigkeit zu einem bestimmten Zeitpunkt ist durch die Summe der Aufenthaltswahrscheinlichkeiten in den Ausfallzuständen zu diesem Zeitpunkt gegeben.

Wenn wie in Beispiel 7.1 Ausfallverteilungen mit nicht-konstanten Ausfallraten verwendet werden, sind die Transitionsraten zeitabhängig. Das macht die Integration erheblich aufwändiger, da nun die zur Integration von steifen Differenzialgleichungssystemen benötigte Jakobi-Matrix bei jedem Zeitschritt mindestens einmal invertiert werden muss.

Beispiel 7.2 Abbildung 39 zeigt das Markov-Modell, welches die Struktur des Fehlerbaums aus Beispiel 7.1 abbildet.

Abbildung 39: Markov Modell mit Berechnung der Unzuverlässigkeit

Die Ergebnisse sind praktisch identisch zu denen, die in Beispiel 7.1 mit Fehlerbäumen berechnet wurden.

Berechnungen zur Funktionalen Sicherheit Größen, Formeln und Methoden

7 Unzuverlässigkeit von komplexen Funktionen

7.1 Berechnung mit Fehlerbäumen

7.2 Berechnung mit Markov Modellen

Berechnungen zur Funktionalen Sicherheit
Größen, Formeln und Methoden