Berechnungen zur Funktionalen Sicherheit
Größen, Formeln und Methoden

5 Nichtverfügbarkeit von komplexen Funktionen

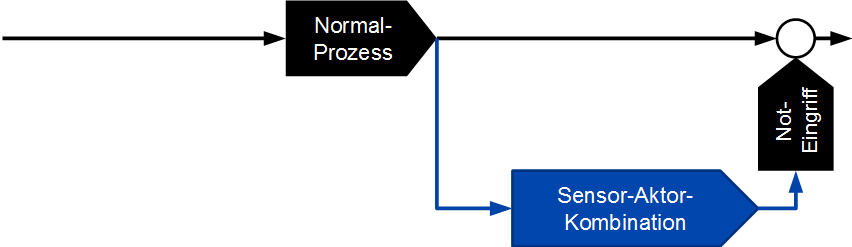
Die Nichtverfügbarkeit ist die wesentliche Größe für Sicherheitsfunktionen, die nur selten benötigt werden. Beispiele für einfache Komponenten, die solche Sicherheitsfunktionen wahrnehmen, sind Leitungsschutzschalter (soll bei Überstrom auslösen), Überdruckventile (soll bei Überdruck aufmachen) oder Deckensprinkler (soll bei zu hoher Temperatur Wasser freigeben). Ihre funktionale Architektur ist in 11 dargestellt.

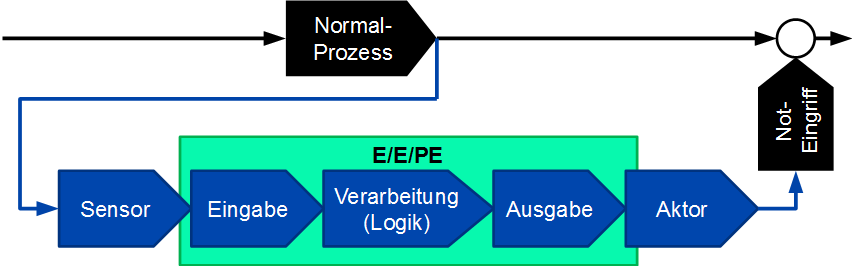
Selbstverständlich gibt es auch komplexere Systeme, die selten benötigte Sicherheitsfunktionen wahrnehmen, heutzutage meist computergesteuert. Beispiele sind Überwachungs- und Notfallsysteme in der chemischen Industrie oder in Kraftwerken, Brandmelde- und Brandbekämpfungsanlagen, Entrauchungsanlagen, Evakuierungssysteme etc. Ihre Architektur ist beispielhaft in Abbildung 12 dargestellt. Der Begriff „Prozess “ ist dabei sehr weit gefasst, das kann einfach der normale Betrieb eines Gebäudes, einer Apparatur oder einer Maschine sein.

Im Normalfall bekommt man von der Existenz der Sicherheitsfunktion(en) nichts mit. Erst im Anforderungsfall (falls dieser überhaupt jemals eintritt) zeigt sich, ob die Sicherheitsfunktion tatsächlich verfügbar ist. ⁴ Ein sicherheitskritischer Fehler (also einer, der die Sicherheitsfunktion im Anforderungsfall verhindert) ist nur erkennbar, wenn die Komponente bzw. das System regelmäßig getestet wird ⁵ oder eben wenn sie im Anforderungsfall nicht funktioniert.

Die Nichtverfügbarkeit ist praktisch immer eine zeitabhängige Funktion \(Q(t)\). Falls es keine Ereignisse mit konstanter Nichtverfügbarkeit gibt, ist die Nichtverfügbarkeit eines Systems \(Q_\mathrm {sys}\) zur Zeit \(t=0\) null. Nur wenn es Ereignisse mit konstanter Nichtverfügbarkeit gibt, kann \(Q_\mathrm {sys}\) schon bei \(t=0\) größer null sein. In jedem System wird es Komponenten geben, die mindestens einen Ausfallsmodus haben, der nicht sofort erkennbar ist. Die Nichtverfügbarkeit wird daher bis zum nächsten Test monoton ansteigen, und unmittelbar nach einem Test auf einen kleineren Wert (im Fall vollständiger Tests auf den Wert bei \(t=0\)) abfallen. Gibt es Ausfälle, die nie erkannt werden, steigt die Nichtverfügbarkeit zumindest im Mittel bis zum Einsatzende des Systems an.

Da niemals bekannt ist, zu welchem Zeitpunkt die Sicherheitsfunktion benötigt wird, interessiert immer nur der Mittelwert der Nichtverfügbarkeit über die Lebenszeit des Prozesses oder des Sicherheitssystems:

\begin{equation} \label {eq:q_mean_} \overline {Q}=\frac {1}{T_{\mathrm {Life}}}\int \limits _0^{T_{\mathrm {Life}}} Q(t) dt \end{equation}

In [IEC 61508] wird dieser Mittelwert \(\overline {Q}\) als Probability of Failure on Demand (kurz PFD) bezeichnet.

⁴ Unter Umständen zeigt sich dann auch erst, ob die Sicherheitsfunktion korrekt ausgelegt ist, also beispielsweise die Aktoren richtig dimensioniert sind, aber das ist nicht Gegenstand der funktionalen Sicherheit

⁵ für bestimmte Komponenten mag dabei auch eine visuelle Inspektion ausreichen

5.1 Berechnung mit Fehlerbäumen

Häufig wird das Sicherheitssystem mit Hilfe von Fehlerbäumen modelliert. Diese sind für die Modellierung solcher Systeme sehr gut geeignet, und die Nichtverfügbarkeit des Systems \(\overline {Q_{\mathrm {sys}}}\) kann sehr einfach und mathematisch exakt berechnet werden (natürlich vorausgesetzt, dass die Nichtverfügbarkeiten der Komponenten bekannt sind).

Wenngleich letztlich nur der Mittelwert der Nichtverfügbarkeit interessiert, so muss gemäß Formel (51) dennoch die zeitabhängige Funktion an ausreichend vielen Stützstellen berechnet und über diese integriert werden.

Die Basis-Ereignisse eines Fehlerbaums modellieren die Komponenten mit ihren Ausfällen sowie gegebenenfalls die Maßnahmen zur Wiederherstellung. Das Standard-Modell für ein Basis-Ereignis ist das sogenannte „wiederherstellbare Ereignis“, auch als testbares oder reparierbares Ereignis bezeichnet, siehe Anhang A.1. Dieses Modell beschreibt eine (konstante) Ausfallrate und eine (mittlere) Detektionszeit sowie gegebenenfalls auch die Reparaturzeit. Wenn der Ausfall nicht durch Diagnose oder Tests erkannt wird, also bis zum Ende der Einsatzzeit im System enthalten bleibt, muss das Ereignis mit dem Modell „nicht-wiederherstellbares Ereignis“ gemäß Anhang A.2 beschrieben werden. In diesem Fall sind auch nicht-konstante Ausfallraten möglich. Manchmal ist die Nichtverfügbarkeit im Anforderungsfall auch weder von einer Zeit seit einem letzten Test noch vom Alter des Systems abhängig, oder das Ereignis beschreibt gar keinen Ausfall, sondern die Wahrscheinlichkeit des Vorhandenseins einer externen Randbedingung oder die Wahrscheinlichkeit eines Bedienfehlers. Dann ist die Nichtverfügbarkeit eine Konstante (Anhang A.3).

Als logische Verknüpfungen kommen fast ausschließlich UND und ODER zum Einsatz, darum sollen auch nur diese hier betrachtet werden. ⁶

Auch wenn man heute zur Berechnung Binäre Entscheidungsdiagramme (engl. Binary Decision Diagrams, kurz BDD) verwendet, so soll dennoch die Berechnung zunächst mithilfe von Minimalschnitten (engl. Minimal Cut-Sets, MCS) erklärt werden.

Ein Minimalschnitt ist eine Kombination von Basis-Ereignissen, die zum Eintreten des Top-Ereignisses (beispielweise dem Ausfall einer Sicherheitsfunktion) notwendig und hinreichend ist. Bei sogenannten kohärenten Fehlerbäumen – das sind Fehlerbäume, die keine negierenden Gatter wie NOT, XOR, NAND etc. enthalten – gibt es genau einen Satz von Minimalschnitten. Bei inkohärenten Fehlerbäumen spricht man von Prim-Implikanten anstelle von Minimalschnitten, und es gibt im Allgemeinen mehrere mögliche Sätze von Prim-Implikanten. Da negierende Gatter praktisch nie benötigt werden, werden sie im Folgenden nicht erwähnt.

⁶ Sogenannte Mehrheitsentscheider (M-aus-N) sind nichts anderes als eine Abkürzung für ein ODER-Gatter über mehreren UND-Gattern, diese sind also eingeschlossen. Siehe hierzu Abschnitt 6.1.6.

5.1.1 Nichtverfügbarkeit einer UND-Verknüpfung

Eine UND-Verknüpfung von zwei oder mehr Basis-Ereignissen führt zu einem Minimalschnitt mit eben diesen Basis-Ereignissen. Eine UND-Verknüpfung von Zweigen eines Baums führt in der Regel auch zu längeren Minimalschnitten, die genaue Anzahl und Länge hängt von der Struktur der verknüpften Zweige ab.

Die Wahrscheinlichkeit, dass ein Minimalschnitt zu einer Zeit \(t\) erfüllt ist, also die von einem Minimalschnitt ausgehende Nichtverfügbarkeit, beträgt

\begin{equation} Q_{\mathrm {MCS}}(t)=\prod \limits _{j=1}^m Q_j(t) \label {eq:q_MCS} \end{equation}

wobei \(m\) die Anzahl der Basisereignisse in diesem Minimalschnitt ist. Die Anzahl \(m\) bezeichnet man als Ordnung des Minimalschnitts.

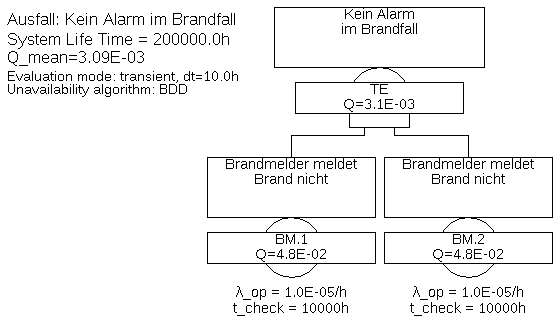
Beispiel 5.1 In einem Zimmer befinden sich zwei Brandmelder. Jeder hat eine Ausfallrate von \(\lambda =\SI {1e-5}{\per \hour }\). Die beiden Brandmelder werden etwa alle \(\SI {10000}{\hour }\) gleichzeitig getestet und im Fehlerfall umgehend ersetzt. Mit welcher Wahrscheinlichkeit meldet nicht mindestens einer von ihnen im Brandfall den Brand?

Abbildung 13 zeigt den entsprechenden Fehlerbaum. Er besteht aus zwei Basis-Ereignissen vom Typ „wiederherstellbares Ereignis“, welche durch ein UND-Gatter verknüpft sind.

Abbildung 13: Redudante Brandmelder

Es gibt nur einen Minimalschnitt, nämlich {BM.1 & BM.2}. Da er zwei Elemente (Literale) enthält, ist es ein Minimalschnitt zweiter Ordnung. Folglich gilt mit Formeln (52) für die Nichtverfügbarkeit des Minimalschnitts und (39) für die Nichtverfügbarkeiten der Brandmelder
\(\seteqnumber{0}{}{52}\)
\begin{equation*} Q_{\mathrm {sys}}(t) = Q_{\mathrm {BM.1}}(t) \cdot Q_{\mathrm {BM.2}}(t) = Q_{\mathrm {BM}}^2(t) = \left ( 1-\mathrm {e}^{-\lambda (t \bmod T_\mathrm {test})} \right )^2 = 1 - 2\mathrm {e}^{-\lambda (t \bmod T_\mathrm {test})} + \mathrm {e}^{-2 \lambda (t \bmod T_\mathrm {test})} \end{equation*}

Mit den genannten Größen ergibt sich eine Periodizität mit einer Periodendauer von \(\SI {10 000}{\hour }\), der genaue Verlauf ist in Abbildung 14 dargestellt.

Abbildung 14: Zeitlicher Verlauf der Nichtverfügbarkeit zweier gleichartig redundanter Komponenten, die regelmäßig zu denselben Zeiten getestet werden (Ausschnitt)

Aufgrund der Periodizität genügt es, den Mittelwert über eine Periode zu berechnen:
\(\seteqnumber{0}{}{52}\)
\begin{align*} \begin{split} \overline {Q}&=\frac {1}{T_{\mathrm {Life}}}\int \limits _0^{T_{\mathrm {Life}}} Q(t)\,dt =\frac {1}{\SI {10000}{\hour }} \int \limits _{\SI {0}{\hour }}^{\SI {10000}{\hour }} 1 - 2\mathrm {e}^{-\lambda t} + \mathrm {e}^{-2 \lambda t}\,dt \\ &=\frac {1}{\SI {10000}{\hour }} \left [ t+\dfrac {2\mathrm {e}^{-\lambda t}}{\lambda } - \dfrac {\mathrm {e}^{-2\lambda t}}{2\lambda } \right ]_{\SI {0}{\hour }}^{\SI {10000}{\hour }} =\num {0.00309459}... \approx \num {3.1e-3} \end {split} \end{align*} Die System-Einsatzzeit (Lebenszeit) spielt aufgrund der regelmäßigen Tests keine Rolle.

Der Leser mag durch eigene Rechnung feststellen, dass bei Verwendung der vereinfachten Formel \(Q_{\mathrm {BM}}(t)\lessapprox \lambda \cdot t\) anstelle der hier verwendeten exakten Formel \(Q_{\mathrm {BM}}(t)=1-\exp (-\lambda t)\) praktisch dasselbe Ergebnis herauskommt.

5.1.2 Nichtverfügbarkeit einer ODER-Verknüpfung

Eine ODER-Verknüpfung von zwei oder mehr Basis-Ereignissen führt zu entsprechend vielen Minimalschnitten. Eine ODER-Verknüpfung von Zweigen eines Baums führt in der Regel auch zu mehreren Minimalschnitten, die genaue Anzahl hängt von der Struktur der verknüpften Zweige ab.

Die Gesamt-Nichtverfügbarkeit des Systems ist näherungsweise die Summe der Nichtverfügbarkeiten der \(n\) Minimalschnitte:

\begin{equation} Q_{\mathrm {sys}}(t) \lessapprox \sum \limits _{i=1}^{n_\mathrm {MCS}} Q_{\mathrm {MCS},i}(t) = \sum \limits _{i=1}^{n_\mathrm {MCS}} \left ( \prod \limits _{j=1}^{m_{\mathrm {Lit},i}} Q_j(t) \right ) \label {eq:q_sys_approx} \end{equation}

Diese Formel ist eine Näherung, die nur gilt, wenn die Einzel-Nichtverfügbarkeiten sehr klein sind.

Eine bessere Näherung, die sich fast ebensoleicht berechnen lässt, ist die Esary-Proschan-Formel:

\begin{equation} Q_{\mathrm {sys}}(t) \lessapprox 1-\prod \limits _{i=1}^{n_\mathrm {MCS}} \left ( 1-Q_{\mathrm {MCS},i}(t) \right ) \label {eq:q_sys_esary_proschan} \end{equation}

Diese Näherung kann in der Praxis gut verwendet werden, da sie immer konservativ ist (also \(Q_{\mathrm {sys}}(t)\) nie zu klein schätzt), für kleine Nichtverfügbarkeiten gegen das exakte Ergebnis tendiert, und für große Nichtverfügbarkeiten nicht größer als eins wird. ⁷

Das exakte Ergebnis erhält man durch disjunkte Zerlegung der Minimalschnitte. Ein Verfahren zur disjunkten Zerlegung ist in [EN 61025] beschrieben. Dieses eignet sich jedoch nur für sehr kleine Fehlerbäume ⁸.

Binäre Entscheidungsdiagramme (BDDs) können auch für sehr große Fehlerbäume mit geringem Aufwand erstellt werden, ohne dass überhaupt Minimalschnitte ermittelt werden müssen. Zudem implizieren sie bei der Berechnung schon die Disjunktion. Sie erlauben daher eine exakte Berechnung der Nichtverfügbarkeit mit deutlich geringerem Aufwand als die Näherung über Minimalschnitte. Und schließlich sind BDDs die mit Abstand schnellste Methode zum Ermitteln der Minimalschnitte. Moderne FTA-Werkzeuge nutzen daher BDDs für alle Operationen.

⁷ über Minimal-Pfade kann man auch eine untere Grenze schätzen, diese ist jedoch bei praktischen Aufgaben so weit vom tatsächlichen Wert entfernt, dass sie bedeutungslos ist

⁸ und für diese ist die Überschneidung der Minimalschnitte bei korrekt ausgelegten Systemen ohnehin gering, eine disjunkte Zerlegung also unnötig

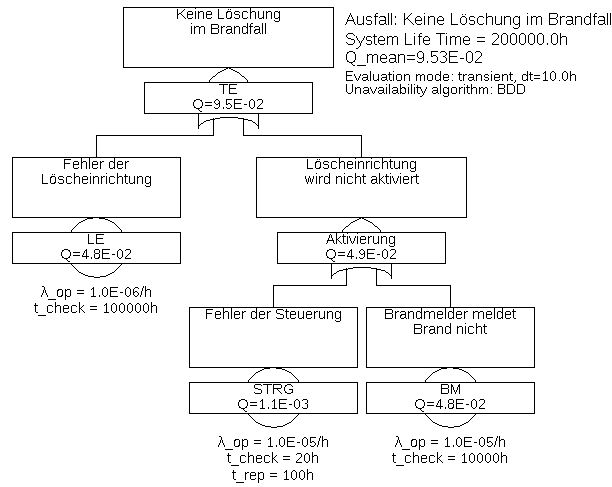
Beispiel 5.2 Eine automatische Brandlöschanlage besteht im Prinzip aus einem Brandmelder (BM), einer Steuerung (STRG) und einer Löscheinheit (LE). Ein Brand wird nur dann gelöscht, wenn diese drei Einheiten im Falle eines Brandes funktionieren.

Abbildung 15: Brandlöschanlage

Dies wird durch den in Abbildung 15 dargestellten Fehlerbaum modelliert. Mathematisch könnte man alle drei Basisereignisse direkt unter das obere ODER-Gatter setzen, dies würde jedoch der FTA-Regel „Top-Down-Entwurf “ widersprechen. Diese Regel besagt, dass ein Fehlerbaum stets vom Top-Ereignis aus nach unten entwickelt werden soll und ist eine der wichtigsten Regeln überhaupt. Und wenn man überlegt, warum die Löschanlage nicht löscht, kann das unmittelbar nur daran liegen, dass sie selbst nicht funktioniert oder dass sie nicht aktiviert wird. Steuerung und Brandmelder kommen erst bei der Frage ins Spiel, warum die Löschanlage nicht aktiviert wird, also eine Ebene tiefer.

Es gibt drei Minimalschnitte, nämlich {LE}, {STRG} und {BM}. Alle drei sind erster Ordnung. Verwendet man die Näherungsformel (53) für die System-Nichtverfügbarkeit, so erhält man
\(\seteqnumber{0}{}{54}\)
\begin{equation*} Q_{\mathrm {sys}}(t) \lessapprox Q_{\mathrm {LE}}(t) + Q_{\mathrm {STRG}}(t) + Q_{\mathrm {BM}}(t) \end{equation*}

und damit für den Mittelwert
\(\seteqnumber{0}{}{54}\)
\begin{equation*} \overline {Q_{\mathrm {sys}}} \lessapprox \overline {Q_{\mathrm {LE}}} + \overline {Q_{\mathrm {STRG}}} + \overline {Q_{\mathrm {BM}}} \end{equation*}

Mit den in Abbildung 15 erwähnten Werten und den Näherungsformeln (41) bzw. (47) erhält man schließlich
\(\seteqnumber{0}{}{54}\)
\begin{align*} \begin{split} \overline {Q_{\mathrm {sys}}} &\approx \num {0.5} \lambda _{\mathrm {LE}} T_{\mathrm {Test,LE}} + \lambda _{\mathrm {STRG}} ( \num {0.5}\,T_{\mathrm {Test,STRG}} + T_{\mathrm {MRT,STRG}} ) + \num {0.5} \lambda _{\mathrm {BM}} T_{\mathrm {Test,BM}}\\ &= \num {0.05} + \num {0.0011} + \num {0.05} = \num {0.1011} \end {split} \end{align*} Diese Näherungsrechnung weicht vom (hier nicht hergeleiteten) exakten Wert \(Q=\num {0.0953}...\) um nur 5% ab — eine für die Praxis längst ausreichende Genauigkeit.

Verwendet man die Abschätzung nach Esary-Proschan (54), so erhält man
\(\seteqnumber{0}{}{54}\)
\begin{equation*} Q_{\mathrm {sys}}(t) \lessapprox 1-\left [ ( 1-Q_{\mathrm {LE}}(t) ) \cdot ( 1-Q_{\mathrm {STRG}}(t) ) \cdot ( 1-Q_{\mathrm {BM}}(t) ) \right ] \end{equation*}

Mit denselben Näherungen wie zuvor für die Einzel-Nichtverfügbarkeiten ergibt sich für die mittlere System-Nichtverfügbarkeit
\(\seteqnumber{0}{}{54}\)
\begin{align*} \begin{split} \overline {Q_{\mathrm {sys}}} &\lessapprox 1-\big [ ( 1-\num {0.5} \lambda _{\mathrm {LE}} T_{\mathrm {Test,LE}} ) \\ &\qquad \quad \cdot ( 1-\lambda _{\mathrm {STRG}} ( \num {0.5}\,T_{\mathrm {Test,STRG}} + T_{\mathrm {MRT,STRG}} ) ) \cdot ( 1- \num {0.5} \lambda _{\mathrm {BM}} T_{\mathrm {Test,BM}} ) \big ] \\ &=1-\left [(1-\num {0.05})\cdot (1-\num {0.0011})\cdot (1-\num {0.05})\right ]=\num {0.09849}... \end {split} \end{align*} Diese Näherung weicht vom exakten Wert \(Q=\num {0.0953}...\) um nur 3% ab.

5.1.3 Nichtverfügbarkeit von Kombinationen von UND- und ODER-Verknüpfungen

Für so einfache Systeme wie in den bisherigen Beispielen wird man kaum einen Fehlerbaum verwenden. Praktisch bestehen Fehlerbäume immer aus einer Mehrzahl von UND- und ODER-Gattern, welche oft eine Vielzahl von Basis-Ereignissen verknüpfen.

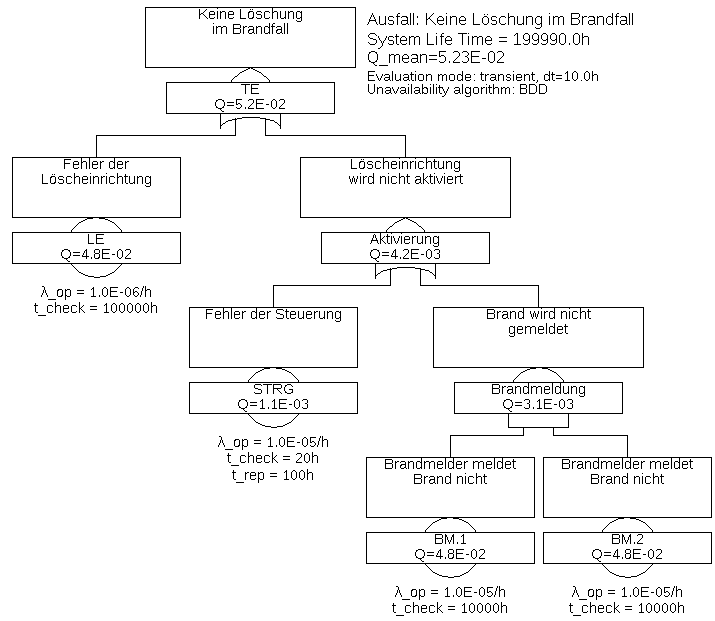
Beispiel 5.3 Abschließend sollen die beiden vorherigen Beispiele kombiniert werden. Die beiden Rauchmelder seien dabei wieder redundant, also nebeneinander montiert und so verschaltet, dass einer von beiden ausreicht, um einen Brand zu melden.

Der Fehlerbaum ist in Abbildung 16 gezeigt.

Abbildung 16: Brandlöschanlage mit redundanten Sensoren

Die drei Minimalschnitte sind: {LE}, {STRG}, {BM.1 & BM.2}

Gemäß Näherungsformel (53) gilt für die System-Nichtverfügbarkeit etwa:
\(\seteqnumber{0}{}{54}\)
\begin{equation*} Q_{\mathrm {sys}}(t) \lessapprox \sum \limits _{j=1}^n Q_{\mathrm {MCS},i}(t) = Q_{\mathrm {LE}}(t) + Q_{\mathrm {STRG}}(t) + Q_{\mathrm {BM.1}}(t) \cdot Q_{\mathrm {BM.2}}(t) \end{equation*}

Für den interessierten und mit BDDs vertrauten Leser soll der Vollständigkeit halber noch das BDD angegeben werden.

Wählt man die Variablenordnung Löscheinrichtung (LE), Steuerung (STRG), Brandmelder.1 (BM.1), Brandmelder.2 (BM.2), so erhält man das in Abbildung 17 gezeigte binäre Entscheidungsdiagramm BDD.

Abbildung 17: BDD für die Brandlöschanlage mit redundanten Sensoren

Aus dem BDD kann direkt eine exakte Formel für die System-Nichtverfügbarkeit abgeleitet werden:
\(\seteqnumber{0}{}{54}\)
\begin{equation*} Q_{\mathrm {sys}}(t) = Q_{\mathrm {LE}}(t) + (1-Q_{\mathrm {LE}}(t)) \cdot \left [ Q_{\mathrm {STRG}}(t) + (1-Q_{\mathrm {STRG}}(t)) \cdot \left ( Q_{\mathrm {BM.1}}(t) \cdot Q_{\mathrm {BM.2}}(t) \right ) \right ] \end{equation*}

In dieser Formel sind automatisch alle Ereignisse disjunkt. Es sei angemerkt, dass sich bei anderen Variablenordnungen andere Formeln ergeben, diese sind jedoch alle mathematisch äquivalent.

Vergleicht man im letzten Beispiel die exakte Formel mit der Näherungsformel, so sieht man unmittelbar, dass die Näherungsformel (53) für alle Fehlerbäume, die keine negierenden Gatter enthalten, immer ein zu großes Ergebnis liefert. Für kleine Fehlerbäume ist der Unterschied bei allen korrekt ausgelegten Systemen⁹ vernachlässigbar, bei großen Fehlerbäumen mit vielen Tausend Minimalschnitten kann der Fehler jedoch selbst dann sehr groß werden. Daher können große Fehlerbäume praktisch nur mit BDDs berechnet werden, zumal schon die Ermittlung von Minimalschnitten bei großen Fehlerbäumen praktisch nur mit Hilfe von BDDs (noch besser mit ternären Entscheidungsdiagrammen) möglich ist.

⁹ korrekte Auslegung bedeutet, dass die Testintervalle den Ausfallraten angemessen sind, so dass alle Nichtverfügbarkeiten jederzeit sehr klein sind

5.1.4 Transiente und stationäre Berechnung, Rechnen mit Mittelwerten

Im Allgemeinen muss zur Ermittlung der mittleren Nichtverfügbarkeit eines Systems das Integral gemäß Formel (51) berechnet werden, so wie in Beispiel 5.1 gezeigt. Praktisch bedeutet das, dass der Fehlerbaum für viele Zeitpunkte berechnet werden muss, was für große Fehlerbäume auch mit modernen Rechnern einige Zeit in Anspruch nehmen kann. Hierbei kann natürlich eine eventuell vorhandene Periodizität ausgenutzt werden, wie ebenfalls in Beispiel 5.1 geschehen. Gibt es keine Periodizität (zum Beispiel weil es mindestens ein Ereignis ohne regelmäßige Tests gibt), so wird sich kein quasi-stationärer Zustand ¹⁰ einstellen. In diesem Fall muss die Berechnung immer gemäß Formel (51), also numerische Integration über die Lebenszeit, erfolgen. Da diese Berechnung auch transiente, also nicht periodische Vorgänge korrekt berücksichtigt, wird sie auch als transiente Berechnung bezeichnet, in [ASTRA TM] einfach als zeitabhängige Berechnung.

Um die Rechenzeit zu verringern, kann man auf die Idee kommen, den Fehlerbaum nur einmal mit den Mittelwerten der Nichtverfügbarkeiten der Basis-Ereignisse zu berechnen. Diese Rechnung geht von einem eingeschwungenen quasi-stationären Zustand aus, und wird daher auch als stationäre Berechnung bezeichnet.

Die Rechnung mit Mittelwerten ist jedoch auch im eingeschwungenen Zustand nicht korrekt, denn hierdurch würden Integral und Produkt in der Reihenfolge vertauscht, was mathematisch falsch ist:

\begin{equation*} \overline {Q_{\mathrm {MCS}}} = \frac {1}{T_{\mathrm {Life}}}\int \limits _0^{T_{\mathrm {Life}}} Q(t)\,dt = \frac {1}{T_{\mathrm {Life}}}\int \limits _0^{T_{\mathrm {Life}}} \prod _{i=1}^n Q_i(t) \,dt \quad \neq \quad \prod _{i=1}^n \frac {1}{T_{\mathrm {Life}}} \int \limits _0^{T_{\mathrm {Life}}} Q_i(t) \,dt = \prod _{i=1}^n \overline {Q_i} \end{equation*}

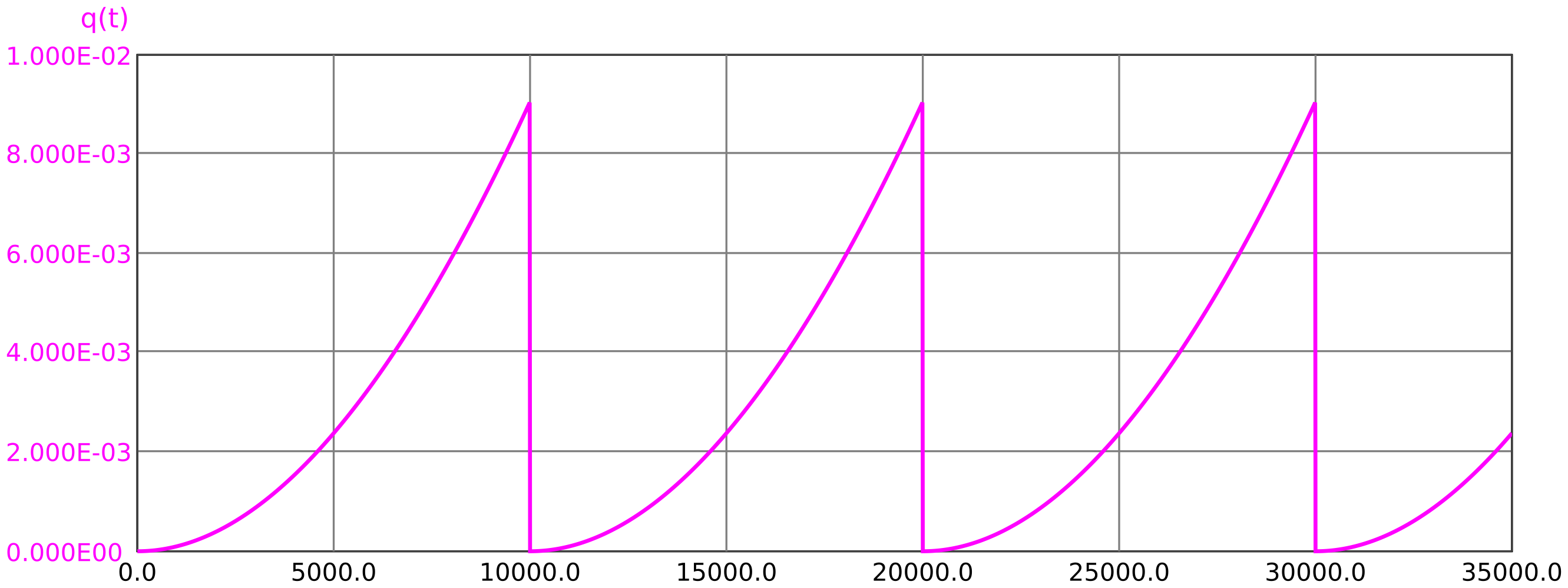
Die Größe des Fehlers, der bei der Berechnung mit Mittelwerten entsteht, hängt von vielen Parametern ab. Im Falle von zwei gleichartigen UND-verknüpften Ereignissen wie in Beispiel 5.1, welche zur selben Zeit getestet werden, ist das berechnete Ergebnis etwa 1/3 zu klein:

\begin{equation*} \overline {Q_{\mathrm {BM.1}}} \cdot \overline {Q_{\mathrm {BM.2}}} \approx \num {4.8e-2} \cdot \num {4.8e-2} \approx \num {2.3e-3}... \neq \num {3.1e-3} \end{equation*}

Der Fehler 1/3 rührt aus der Integration des quadratischen Terms her, der für die in Abbildung 14 deutlich sichtbaren Parabelabschnitte verantwortlich ist. Formelmäßig wird das besonders deutlich, wenn man die Näherungsformel \(Q(t)\lessapprox \lambda \cdot t\) verwendet:

\begin{equation*} \overline {Q_{\mathrm {korrekt}}} = \frac {1}{T}\int \limits _0^T Q_1(t) \cdot Q_2(t)\,dt \approx \frac {1}{T}\int \limits _0^T \lambda t \cdot \lambda t\,dt = \frac {\lambda ^2}{3T} T^3 = \frac {\lambda ^2 T^2}{3} \end{equation*}

\begin{equation*} \overline {Q_{\mathrm {falsch}}} = \frac {1}{T}\int \limits _0^T Q_1(t)\,dt \cdot \frac {1}{T}\int \limits _0^T Q_2(t)\,dt \approx \left ( \frac {1}{T}\int \limits _0^T \lambda t\,dt \right )^2 = \left ( \frac {\lambda }{2T} T^2\right )^2 = \frac {\lambda ^2 T^2}{4} \end{equation*}

Bei höheren Potenzen, also Minimalschnitten höherer Ordnung, wird der relative Fehler noch größer, allerdings ist deren absoluter Beitrag in der Regel nur gering. Eine Berechnung mit Mittelwerten kann in der Praxis also für Überschlagsrechnungen verwendet werden, die abschließende Berechnung sollte aber immer gemäß Formel (51) erfolgen, was eine numerische Integration erforderlich macht.

Es sei angemerkt, dass eine stationäre Berechnung auch mit Maximalwerten anstatt mit Mittelwerten ausgeführt werden kann. In dem Fall ist die ermittelte Nichtverfügbarkeit immer (sehr) konservativ.

¹⁰ quasi-stationär bedeutet, dass die Nichtverfügbarkeit zwar um einen Mittelwert schwanken kann, der Mittelwert sich aber mit der Zeit nicht verändert

5.2 Berechnung mit Markov Modellen

Die System-Nichtverfügbarkeit kann auch mittels Markov-Modellen berechnet werden. Markov-Modelle stellen die Zustände dar, in denen sich ein System befinden kann, sowie die Übergänge (Transitionen) zwischen den Zuständen. Bei klassischen Markov-Modellen werden die Transitionen mittels Übergangsraten beschrieben. Transitionen vom Ursprungszustand weg, also insbesondere Ausfälle, werden meist mit \(\lambda \) abgekürzt. Transitionen in Richtung des Ursprungszustands, also Maßnahmen der Wiederherstellung, werden meist mit \(\mu \) abgekürzt. Damit ist ein Markov-Modell mathematisch durch ein lineares Differenzialgleichungssystem beschrieben:

\begin{equation} \dot {\vec {p}}(t) = A(t)\,\vec {p}(t) \end{equation}

Dabei ist \(A(t)\) die (im Allgemeinen zeitabhängige) Transitionsmatrix und \(\vec {p}\) der Vektor der Aufenthaltswahrscheinlichkeiten der Systemzustände.

Da sich das System zu jeder Zeit in genau einem Zustand befindet, muss die Summer aller Zustandswahrscheinlichkeiten stets eins sein:

\begin{equation} \|\vec {p}(t)\| = \sum _{i=1}^n p_i(t) = 1 \end{equation}

Die Summe der Aufenthaltswahrscheinlichkeiten in den Zuständen \(p_j(t) \in \vec {p(t)}\), in denen die Sicherheitsfunktion nicht gegeben ist, gibt die System-Nichtverfügbarkeit an:

\begin{equation} \label {eq:mm_sum_unavail} Q(t) = \sum _{j=1}^m p_j(t) \end{equation}

Die mittlere Nichtverfügbarkeit ist wieder durch Formel (51) gegeben.

Die Wiederherstellungsrate \(\mu \) wird in der Fachliteratur fast immer als Kehrwert der mittleren Wiederherstellungszeit definiert: ¹¹

\begin{equation} \label {eq:mu} \mu \stackrel {\mathrm {def}}{=} 1 / \mathrm {MTTR} \end{equation}

Für Fehler, die durch regelmäßige Tests entdeckt werden, ergibt sich damit für die Wiederherstellungsrate

\begin{equation} \label {eq:mu_latent} \mu = 1 / \mathrm {MTTR} = \frac {1}{\num {0.5}\cdot T_{\mathrm {test}}} = 2/T_{\mathrm {test}} \end{equation}

¹¹ Dass es sich hierbei tatsächlich um eine Definition und nicht um eine sachlich begründbare Formel handelt, wird in Beispiel 5.4 mit Beispiel 5.5 sichtbar.

Beispiel 5.4 Abbildung 18 zeigt das Markov-Modell für die Brandmeldung mittels redunanter Brandmelder, wie in Beispiel 5.1 betrachtet.

Abbildung 18: Redudante Brandmelder, stationäre Berechnung

Die Ausfallraten \(\lambda \) für die Brandmelder sind jeweils über den Transitionspfeilen angegeben, die Wiederherstellungsraten \(\mu \) jeweils darunter und mit einem kleinen Pfeil für die gegensätzliche Richtung versehen. ¹²

Mit dem Zustandsvektor
\(\seteqnumber{0}{}{59}\)
\begin{equation*} \vec {p}= \begin{pmatrix} \mathrm {OK}\\ \mathrm {BM.1}\\ \mathrm {BM.2}\\ \mathrm {BM.1+BM.2} \end {pmatrix} \end{equation*}

gilt für das lineare Differenzialgleichungssystem
\(\seteqnumber{0}{}{59}\)
\begin{equation} \label {eq:ldgs_red_bm} \begin{pmatrix} -2\lambda & \mu & \mu & 0\\ \lambda & -\mu -\!\lambda & 0 & \mu \\ \lambda & 0 & -\mu -\!\lambda & \mu \\ 0 & \lambda & \lambda & -2\mu \end {pmatrix} \,\vec {p}(t)=\dot {\vec {p}}(t) \end{equation}

¹² Häufig werden separate Linien für die Wiederherstellung dargestellt, die Darstellung mit nur einer Linie erscheint jedoch übersichtlicher.

5.2.1 Stationäre Berechnung

Wenn jeder Ausfall detektierbar ist, gibt es aus jedem Zustand auch eine Transition heraus. Folglich werden sich die Zustände nach beliebig langer Zeit im Gleichgewicht befinden, die zeitliche Ableitung des Zustandsvektors also zu null werden. Sind alle Detektions- und Reparaturzeiten relativ kurz im Verhältnis zur Lebenszeit des Systems, wird das Gleichgewicht nach relativ kurzer Zeit praktisch eingenommen sein.

Die Aufenthaltswahrscheinlichkeiten in diesem stationären Systemzustand kann man leicht berechnen, indem man \(\dot {\vec {p}}(t)=0\) setzt und dann eine beliebige Gleichung durch die Summe der Zustandswahrscheinlichkeiten ersetzt, welche immer eins sein muss.

Da der stationäre Zustand ewig währt, hat der Einschwingvorgang keinen signifikanten Einfluss auf das Integral in Formel (51), der Mittelwert der Nichtverfügbarkeit ist also etwa gleich der Nichtverfügbarkeit im stationären Zustand:

\begin{equation} \overline {Q_{\mathrm {sys}}} \approx Q_{\mathrm {stat}} \end{equation}

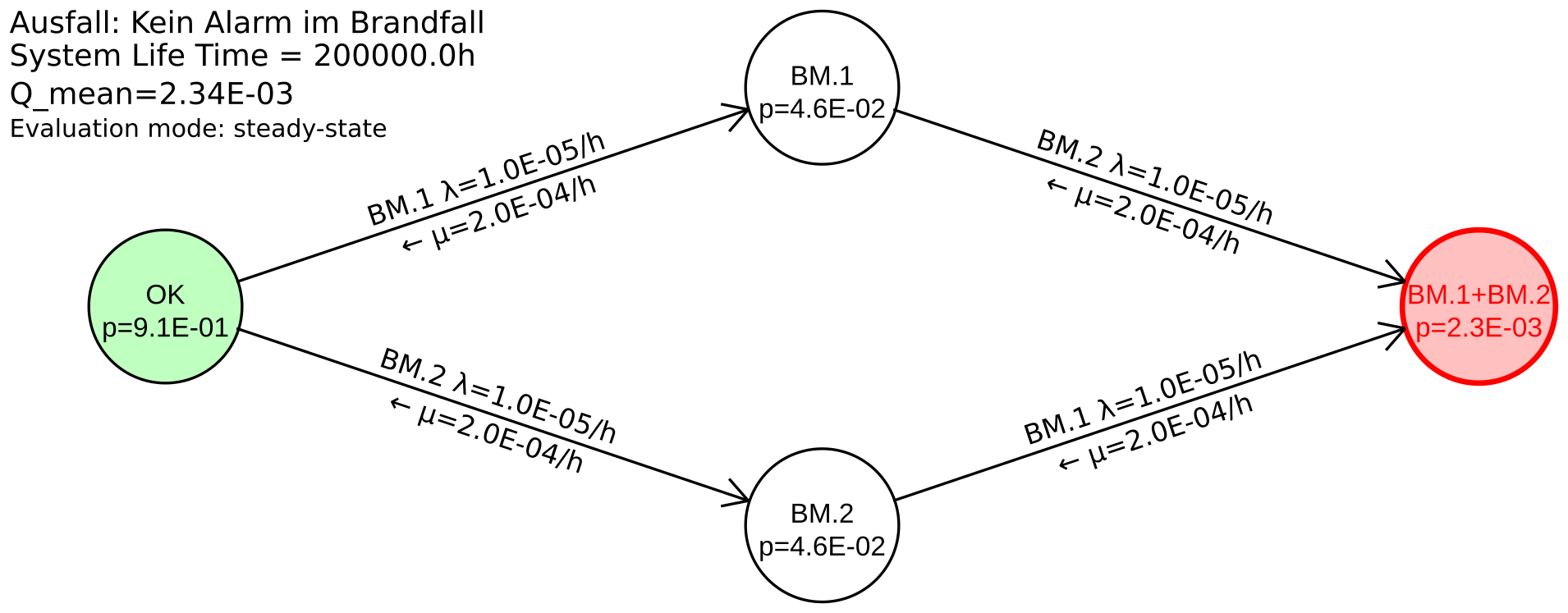
Beispiel 5.5 Ersetzt man in Gleichungssystem (60) die vierte Zeile durch die Summenzeile, so ist die stationäre Lösung durch das folgende lineare Gleichungssystem beschrieben:
\(\seteqnumber{0}{}{61}\)
\begin{equation*} \begin{pmatrix} -2\lambda & \mu & \mu & 0\\ \lambda & -\mu -\!\lambda & 0 & \mu \\ \lambda & 0 & -\mu -\!\lambda & \mu \\ 1 & 1 & 1 & 1 \end {pmatrix} \,\vec {p_{\mathrm {stat}}}= \begin{pmatrix} 0\\ 0\\ 0\\ 1 \end {pmatrix} \end{equation*}

Für den Zustandsvektor im eingeschwungenen Zustand ergibt sich
\(\seteqnumber{0}{}{61}\)
\begin{equation*} \renewcommand *{\arraystretch }{1.8} \vec {p_\mathrm {stat}}= \begin{pmatrix} \mathrm {OK}\\ \mathrm {BM.1}\\ \mathrm {BM.2}\\ \mathrm {BM.1+BM.2} \end {pmatrix} = \begin{pmatrix} \dfrac {{{\mu }^{2}}}{{{\mu }^{2}}+2\lambda \mu +{{\lambda }^{2}}}\\ \dfrac {\lambda \mu }{{{\mu }^{2}}+2\lambda \mu +{{\lambda }^{2}}}\\ \dfrac {\lambda \mu }{{{\mu }^{2}}+2\lambda \mu +{{\lambda }^{2}}}\\ \dfrac {{{\lambda }^{2}}}{{{\mu }^{2}}+2\lambda \mu +{{\lambda }^{2}}} \end {pmatrix} \end{equation*}

Die Nichtverfügbarkeit ist die Aufenthaltswahrscheinlichkeit des Zustands BM.1+BM.2, also \(\overline {Q_{\mathrm {stat}}}=\dfrac {\lambda ^2}{\mu ^2+2\lambda \mu +\lambda ^2}\).

Mit den für Beispiel 5.1 verwendeten Zahlenwerten \(\lambda =\SI {1.0E-5}{\per \hour }\) und \(T_{\mathrm {test}}=\SI {10000}{\hour }\) ergibt sich \(\mu =2/(\SI {10000}{\hour })=\SI {2.0E-4}{\per \hour }\) und damit
\(\seteqnumber{0}{}{61}\)
\begin{equation*} \overline {Q_{\mathrm {stat}}} =\dfrac {(\SI {1.0E-5}{\per \hour })^{2}} {(\SI {2.0E-4}{\per \hour })^2+2\cdot \SI {1.0E-5}{\per \hour }\cdot \SI {2.0E-4}{\per \hour }+(\SI {1.0E-5}{\per \hour })^2} \approx \num {0.0023} \end{equation*}

Die mittlere Nichtverfügbarkeit wurde in Beispiel 5.1 exakt zu \(\overline {Q_{\mathrm {sys}}}=\num {0.003094}...\) berechnetet, das über die stationäre Auswertung des Markov-Modells ermittelte Ergebnis ist also deutlich zu optimistisch. Dies liegt zum Einen daran, dass Formel (58) nur für kontinuierliche Wartung und Reparatur gilt, und Formel (59) immer etwas optimistisch ist, zum Anderen aber auch an der Struktur des Markov-Modells, welches die Realität offensichtlich nicht richtig widerspiegelt — siehe hierzu das nächste Beispiel.

5.2.2 Transiente Berechnung

In vielen praktischen Anwendungen wird der eingeschwungene Zustand nicht einmal ansatzweise erreicht, da die Einsatzdauer zu kurz ist. Falls es Ausfälle gibt, die nicht detektiert oder repariert werden können, gibt es sogar absorbierende Zustände, der stationäre Zustand ist also durch die Kumulation der Aufenthaltswahrscheinlichkeit in einem oder mehreren Ausfallzuständen gegeben, so dass \(Q(t \rightarrow \infty )=1\) gilt ¹³. In diesem Fall ist die stationäre Lösung des Differenzialgleichungssystems uninteressant, statt dessen muss die mittlere Nichtverfügbarkeit mittels Formel (51) während des Übergangs vom Ursprungszustand bis zum Ende der Einsatzzeit des Systems berechnet werden. Dies erfordert eine numerische Integration des Differenzialgleichungssystems.

Die numerische Integration eröffnet Möglichkeiten der Modellierung, die über klassische Markov-Modelle hinausgehen. Insbesondere ist es möglich, zeitlich veränderliche Übergangsraten zu verwenden, und sogar Übergänge zu bestimmten Zeitpunkten zu berücksichtigen. Letzteres wiederum ermöglich die realitätsnahe Berücksichtigung von regelmäßigen Tests.

¹³ absorbierende Zustände sind immer Fehlerzustände, ansonsten ist das Modell nicht korrekt

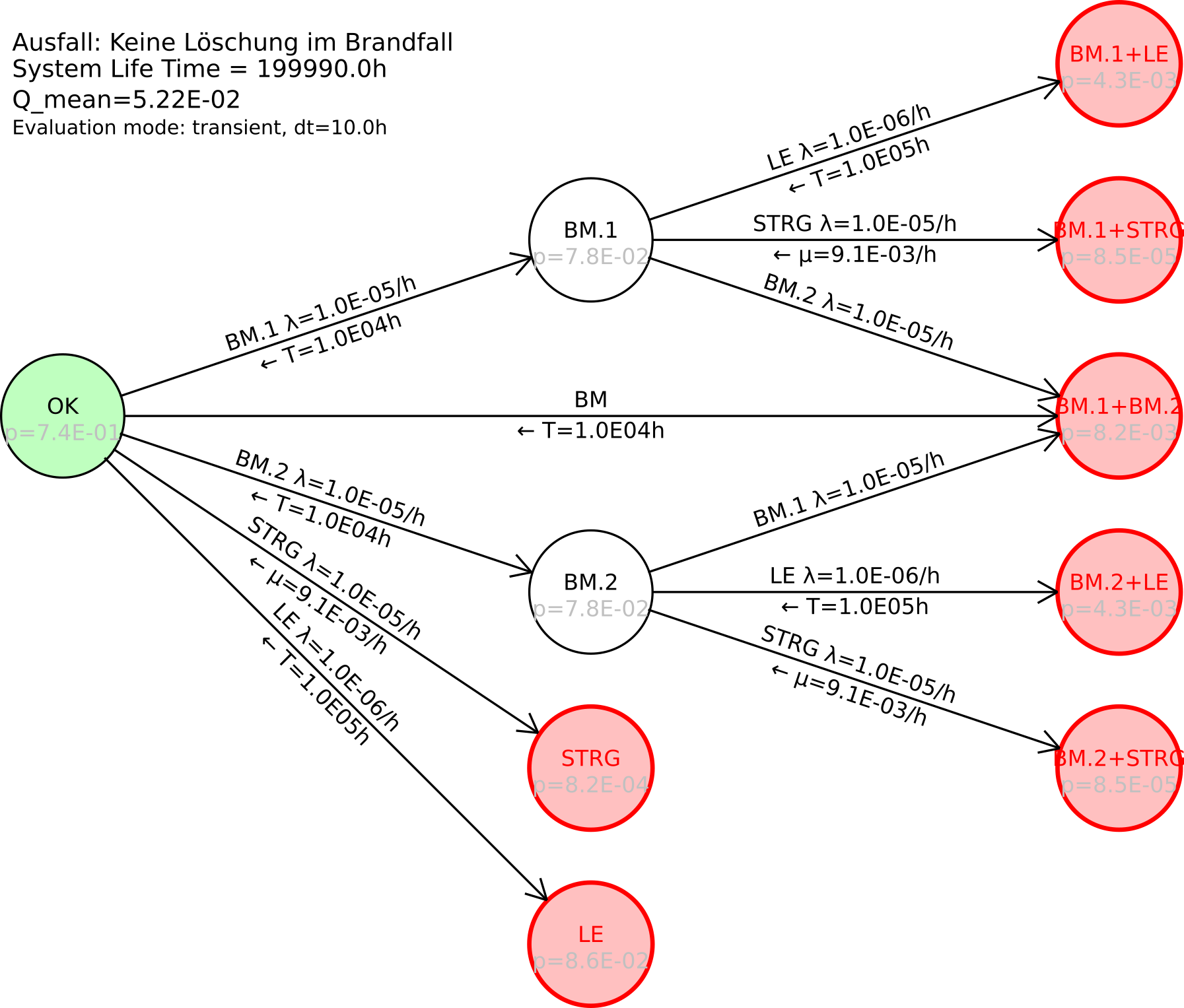
Beispiel 5.6 Abbildung 19 zeigt ein Markov-Modell für die redundanten Brandmelder, bei welchem berücksichtigt wird, dass die Tests und somit die Wiederherstellung nicht kontinuierlich, sondern zu bestimmten Zeitpunkten erfolgt. Außerdem ist berücksichtigt, dass bei Defekt beider Brandmelder (Zustand „BM.1+BM.2“) beide Defekte zur selben Zeit erkannt werden und auch die Reparatur zur selben Zeit stattfindet, also das System in den Ursprungszustand überführt wird.

Abbildung 19: Redundante Brandmelder mit Wiederherstellung zu diskreten Zeitpunkten

Anmerkung: Am Transitionspfeil von „OK“ zu „BM.1+BM.2“ ist keine Ausfallrate angegeben, diese ist daher null. Nur die regelmäßige Wiederherstellung alle 10000 h ist hier relevant, diese steht unter dem Transitionspfeil und ist mit einem kleinen Pfeil nach links angedeutet. Umgekehrt steht unter den Transitionspfeilen von „BM.1“ und „BM.2“ zu „BM.1+BM.2“ keine Wiederherstellung, diese ist also null.

Das Ergebnis dieser Modellierung und der Berechnung mit einer Integrationsschrittweite von 10 Stunden ist \(Q=\num {3.09e-3}\) und stimmt nun praktisch mit dem exakten Wert überein.

Klassische Markov-Modelle mit konstanten Übergangsraten sind für die Berechnung der Nichtverfügbarkeit nur bedingt geeignet, die Ergebnisse sind meist zu optimistisch. Erweiterte Markov-Modelle mit zeitdiskreten Übergängen ermöglichen die realitätsnahe Modellierung und Berechnung und sind daher wesentlich besser geeignet.

Es muss erwähnt werden, dass die Berechnung zeitdiskreter Übergänge eine hinreichend kleine Integrationsschrittweite voraussetzt. Für kleine Testintervalle oder gar kontinuierliche Diagnose müssen konstante Übergangsraten verwendet werden.

Beispiel 5.7 Abbildung 20 zeigt das Markov-Modell für die in Beispiel 5.3 eingeführte Brandlöschanlage mit redunanten Brandmeldern. Die Wiederherstellung der Steuerung STRG wird als kontinuierlicher Übergang behandelt, da die Integrationsschrittweite mit 10 h nur unwesentlich kleiner ist als das Testintervall (20 h). Das Ergebnis stimmt mit dem des Fehlerbaums überein.

Abbildung 20: Brandlöschanlage

Berechnungen zur Funktionalen Sicherheit Größen, Formeln und Methoden