Berechnungen zur Funktionalen Sicherheit
Größen, Formeln und Methoden
6 Ausfallrate von komplexen Funktionen
Die Ausfallrate ist die wesentliche Größe für Sicherheitsfunktionen, die kontinuierlich oder zumindest häufig (quasi-kontinuierlich) benötigt werden. Beispiele für Systeme, die kontinuierlich benötigte Sicherheitsfunktionen implementieren, sind Flugantriebe (sollen immer den geforderten Schub liefern und vor allem nicht fälschlich stehenbleiben), Lageregelungen (sollen immer die vorgegebene Lage sicherstellen), Antriebsregelungen (sollen immer geforderte Drehmomente, Geschwindigkeiten oder Positionen gewährleisten oder nicht zur Unzeit anlaufen), Eisenbahn-Signalanlagen (sollen nie einen zu freigiebigen Signalbegriff anzeigen bzw. einen zu freigiebigen Fahrbefehl geben) aber auch Airbag-Steuerungen (sollen niemals fälschlich den Airbag auslösen), ABS-Steuerungen (sollen den Bremsdruck nie zu stark reduzieren), Zug-Türsteuerungen (sollen die Tür nie zur falschen Zeit öffnen). Sobald die Sicherheitsfunktion versagt, ist unmittelbar eine gefährliche Situation gegeben. Das Wort „unmittelbar“ heißt nicht, dass zwingend ein Schaden entstehen muss, sondern nur, dass bei üblichen externen Bedingungen ein Schaden nicht unwahrscheinlich ist. 14
Beispiele für Systeme, die quasi-kontinuierlich benötigte Sicherheitsfunktionen implementieren, gehören Fahrwerke von Flugzeugen (müssen nur bei der Landung funktionieren, aber die Landung ist unausweichlich), Bremsen von sämtlichen Fahrzeugen (müssen nur bei Bremsanforderung funktionieren, aber die Anforderung kommt fast sicher – nur im Ausnahmefall wird ein Ausrollen möglich sein).
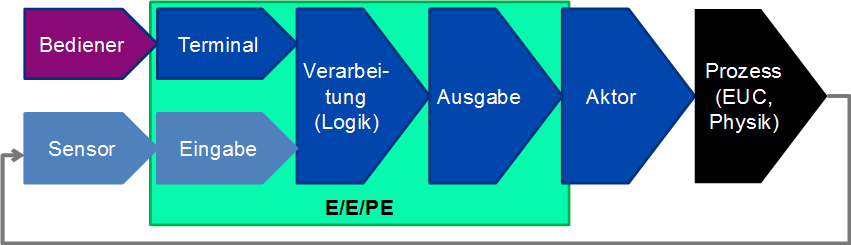
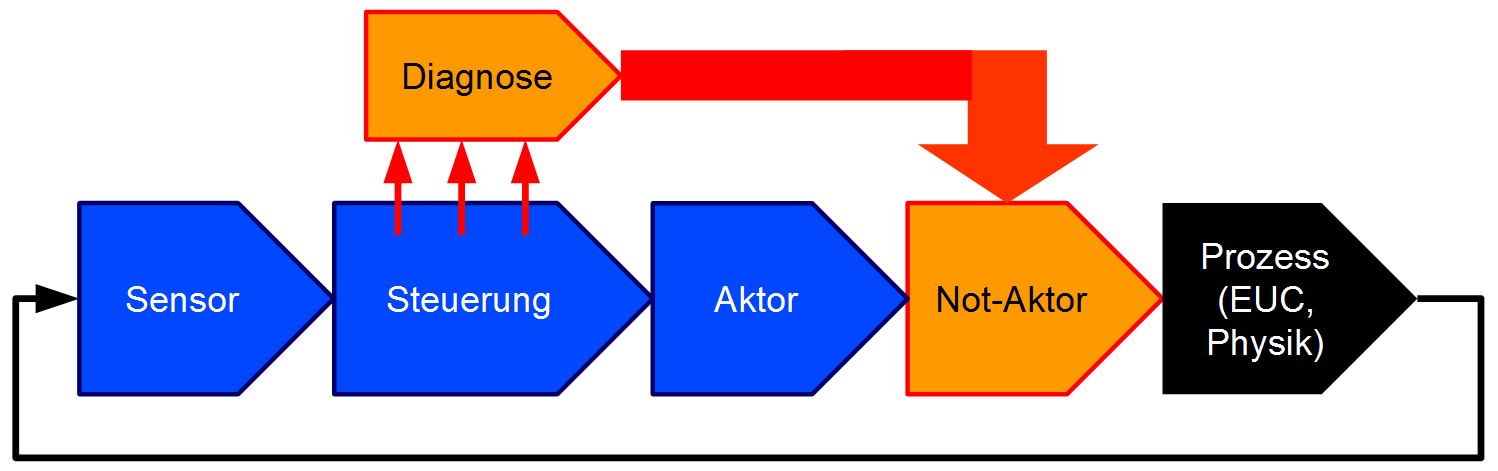
Die prinzipielle Struktur solcher Sicherheitsfunktionen ist in Abbildung 21 dargestellt.
Charakteristisch ist, dass ein Ausfall der Sicherheitsfunktion unmittelbar Einfluss auf das Verhalten des physikalischen Prozesses hat (welcher etwa durch die Bewegungsgleichungen des Fahrzeugs, des Flugzeugs, der Maschine oder die Reaktionsdynamik der Chemikalien und Apparate gegeben ist) und somit zur Gefährdung führt – egal ob der Schaden sofort oder erst nach einer absehbaren Zeit eintritt.
Für kontinuierliche Sicherheitsfunktionen ist der Begriff der Prozessfehlertoleranzzeit (PFTZ, auch Prozesssicherheitszeit genannt) existenziell: Das ist die Zeit, für die die Sicherheitsfunktion verletzt werden darf, ohne dass sich hieraus eine Gefährdung ergibt. Im Fall einer hochdynamischen Antriebsregelung oder einer Lageregelung eines Kampfjets sind dies maximal wenige Millisekunden, im Fall einer Bremse mögen es wenige Sekunden sein, im Fall der Brennstoffzufuhr eines Großkraftwerks vielleicht einige Minuten. Eventuell vorhandene Diagnosemaßnahmen müssen in dieser Zeit den Fehler erkennen und eine adäquate Reaktion initiieren, zum Beispiel eine Sicherheitsabschaltung veranlassen oder die defekte Steuerung isolieren und einen redundanten Steuerpfad aktivieren. Eine reine Fehlermeldung an den Bediener ist bei kontinuierlichen oder quasi-kontinuierlichen Sicherheitsfunktionen in der Regel nicht ausreichend, da der Bediener die Funktion meist nicht wiederherstellen kann, bevor der Schaden eintritt.
Wie bei der Nichtverfügbarkeit ist auch bei der System-Ausfallrate der Mittelwert über die Lebenszeit relevant:
\(\seteqnumber{0}{}{61}\)\begin{equation} \label {eq:overline_h_sys} \overline {h_\mathrm {sys}} = \frac {1}{T_{\mathrm {Life}}} \int \limits _0^{T_{\mathrm {Life}}} h_\mathrm {sys}(t)\,dt \end{equation}
In [IEC 61508] wird dieser Mittelwert \(\overline {h}\) als Probability of Failure per Hour (kurz PFH) bezeichnet. 15
Auf oberster Ebene stellt \(\overline {h_\mathrm {sys}}\) die Gefährdungsrate dar, oft mit HR (für engl. hazard rate) abgekürzt (vgl. [EN 50126]). Wenn es sich bei dem betrachteten System nur um eine Teilfunktion einer Sicherheitsfunktion handelt, wird \(\overline {h_\mathrm {sys}}\) entsprechend als Funktional Failure Rate (FFR) bezeichnet.
\(\overline {h_\mathrm {sys}}\) ist das relevante Maß für die Sicherheit für alle Sicherheitsfunktionen, bei deren Versagen es ohne weitere Bedingungen zu einem Schaden kommen kann (also Sicherheitsfunktionen mit kontinuierlicher oder zumindest häufiger Anforderung).
Anmerkung: Viele Steuerungen nehmen sowohl kontinuierliche Sicherheitsfunktionen wahr, als auch selten benötigte. In diesem Fall muss für die Steuerung sowohl die Nichtverfügbarkeit im Anforderungsfall \(\overline {Q}\) als auch die Häufigkeit eines falschen Kommandos an die Aktorik \(\overline {h}\) bestimmt werden. 16
14 Im Gegensatz zu den Sicherheitsfunktionen mit seltener Anforderungen, die überhaupt erst bei einer unüblichen externen Bedingung (Anforderung) benötigt werden.
15 Anmerkung: Einige Formeln im informativen Anhang B in [IEC 61508-6] sind hierzu nicht konsistent, die Bedeutung der PFH als synonymer Begriff zu \(\overline {h}\) wie hier definiert geht aus den übrigen Teilen der Norm jedoch klar hervor und ist die einzig sinnvolle Definition.
16 In der Regel sind hierfür zwei unterschiedliche Fehlerbäume oder Markov-Modelle nötig, da sich insbesondere die Diagnose bezüglich \(\overline {Q}\) von der für \(\overline {h}\) unterscheidet, und daher andere Basisereignisse (auf Basis einer anderen FMEDA) nötig sind und oft auch andere Gatter.
6.1 Berechnung mit Fehlerbäumen
Die Berechnung der Ausfallrate \(\overline {h}\) ist wesentlich schwieriger als die Berechnung der Nichtverfügbarkeit \(\overline {Q}\), sowohl bezüglich der Aufstellung eines korrekten Fehlerbaums als auch bezüglich der eigentlichen mathematischen Berechnung. Dennoch ist für die meisten Sicherheitsfunktionen die Fehlerbaumanalyse eine geeignete Methode zur Bestimmung der Ausfallrate, und oft die einzige praktikable Methode der Modellierung. Es gibt jedoch leider keinerlei Standardisierung hierfür 17, obwohl die wesentlichen mathematischen Grundlagen schon in [NUREG] erwähnt sind. Daher ist es unerlässlich, dass sich der Analyst intensiv mit den Eigenschaften und Eigenheiten des verwendeten Werkzeugs vertraut macht, und im Zweifelsfall anhand von einfachen Tests von der korrekten Funktion des Werkzeugs überzeugt. Die folgenden Beispiele können Basis solcher Tests sein.
17 [EN 61025] macht keinerlei Angaben, wie Fehlerbäume zur Berechnung von Ausfallraten verwendet werden können – weder bezüglich der Modellierung noch bezüglich der Berechnung).
6.1.1 System ohne Redundanzen
Im einfachsten Fall wird die Sicherheitsfunktion von einer Anzahl \(n\) Komponenten realisiert, welche alle für die Sicherheitsfunktion zwingend erforderlich sind. Fällt eine Komponente aus, fällt die Sicherheitsfunktion aus. Der Fehlerbaum besteht nur aus ODER-Gattern.
-
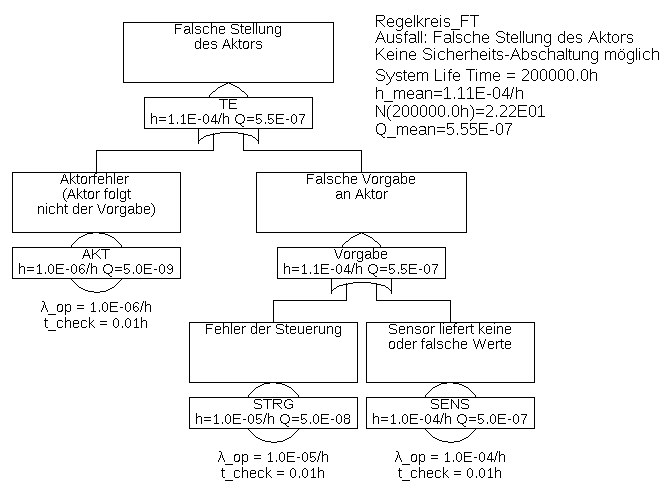
Beispiel 6.1 Der in Abbildung 22 gezeigte Fehlerbaum beschreibt solch ein System, welches aus den Komponenten Sensorik, Logik und Aktorik besteht. Dabei sei angenommen, dass das System zwingend laufen muss, es also keine Möglichkeit einer Not-Abschaltung im Falle von erkannten Fehlern gibt. Die ist häufig der Fall, zum Beispiel kann ein Flugzeug nicht einfach in einen sicheren Zustand gebracht werden, wenn die Geschwindigkeitssensorik als fehlerhaft erkannt wird, denn diese wird für den Weiterflug bis zur Landung zwingend benötigt.
Versagt eine dieser \(n\) Komponenten auf gefährliche Weise 18, ist die Sicherheitsfunktion nicht mehr gewährleistet. Die Minimalschnitte sind offensichtlich: {SENS}, {STRG}, {AKT}.
Für die Gesamtausfallrate gilt die schon aus Abschnitt 3 bekannte Formel
\(\seteqnumber{0}{}{62}\)\begin{equation} h(t) = \sum _{i=1}^n h_i(t) \end{equation}
Da jeder Fehler unmittelbar zum Ausfall führt, spielen weder System-Lebenszeit noch Fehler-Detektions- oder Reparaturzeiten eine Rolle, sondern ausschließlich die Ausfallraten der Komponenten.
Nimmt man für alle Komponenten konstante Ausfallraten an, so ergibt sich mit obiger Formel auch gleich die mittlere Ausfallrate, mit den im Fehlerbaum angegebenen Werten also \(h(t)=\mathrm {const}=\overline {h} =\SI {1.0e-6}{\per \hour }+\SI {1.0e-5}{\per \hour }+\SI {1.0e-4}{\per \hour }=\SI {1.11e-4}{\per \hour }\).
Dieses Beispiel war zweifellos trivial, und kaum jemand würde auf die Idee kommen, für solch ein System überhaupt einen Fehlerbaum (oder ein Markov-Modell) aufzustellen.
6.1.2 System mit Redundanzen
Wirklich interessant und als Modell nahezu unverzichtbar werden Fehlerbäume erst für Systeme mit Redundanzen (Mehrkanaligkeit). Im Fall von Redundanzen führt nicht jeder Einzelausfall zum Versagen der Sicherheitsfunktion, im Fehlerbaum wird also mindestens ein UND-Gatter enthalten sein, und es wird mindestens einen Minimalschnitt geben, der mehr als ein Basis-Ereignis enthält, also eine Ordnung größer eins hat.
-
Beispiel 6.2 In Beispiel 6.1 ist offensichtlich die Sensorik eine Schwachstelle. Daher sollen nun zwei Sensoren in einer redundanten Anordnung verwendet werden, also so, dass beide Sensoren dieselbe physikalische Größe messen. Wie schon in Beispiel 6.1 sei angenommen, dass das System zwingend laufen muss, es also keine Möglichkeit einer Not-Abschaltung im Falle von erkannten Fehlern gibt.
Wenn ein Sensor gar keine Werte oder offensichtlich falsche Werte liefert, kann nun der Messwert des anderen Sensors verwendet werden. Wenn jedoch nicht klar ist, welcher von beiden Sensoren defekt ist, kann die Steuerung auch weiterhin keine korrekte Stellgröße berechnen. Dasselbe gilt auch in dem Fall, dass ein Sensor bekanntermaßen defekt ist, und nun noch der zweite ausfällt, bevor der erste repariert wurde.
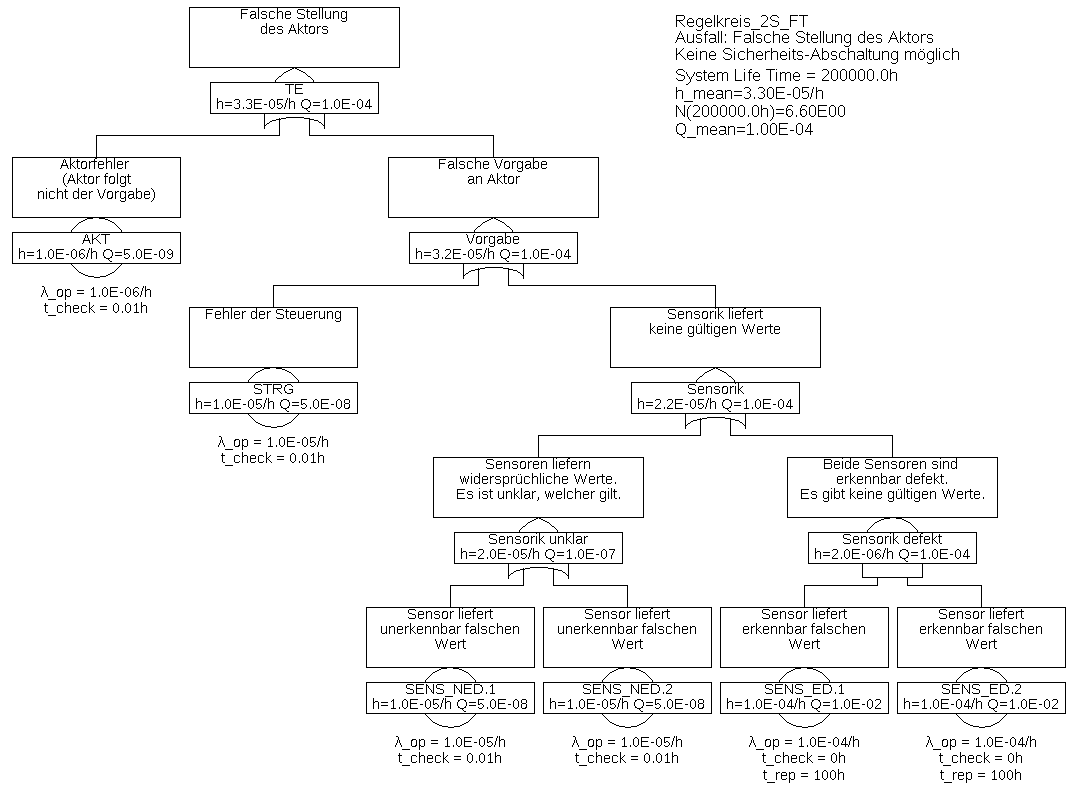
Die Sensoren müssen nun also bezüglich ihrer Fehlermodi unterschieden werden: Es gibt Defekte der Sensoren, die von der Steuerung erkannt werden können (SENS_ED, wie beispielsweise Drahtbruch), und solche, die nicht von der Steuerung erkannt werden können (SENS_NED). Der hierzu gehörige Fehlerbaum ist in Abbildung 23 gezeigt.
Die Minimalschnitte sind:
-
• {AKT}
-
• {STRG}
-
• {SENS_NED.1}
-
• {SENS_NED.2}
-
• {SENS_ED.1 & SENS_ED.2}
Die Frage ist nun, wie die Eintrittsrate \(h_{\mathrm {MCS}}(t)\) des Minimalschnitts {SENS_ED.1 & SENS_ED.2} berechnet werden kann. Die Aussage dieses Minimalschnitts ist folgende:
-
1. Sensor 1 ist bekanntermaßen defekt (also nicht verfügbar, \(Q_\mathrm {SENS\_ED.1}\)), und nun fällt auch noch Sensor 2 aus (mit Ausfallrate \(\lambda _\mathrm {SENS\_ED.2}\))
ODER -
2. Sensor 2 ist bekanntermaßen defekt (also nicht verfügbar, \(Q_\mathrm {SENS\_ED.2}\)), und nun fällt auch noch Sensor 1 aus (mit Ausfallrate \(\lambda _\mathrm {SENS\_ED.1}\)).
Für den Minimalschnitt gilt daher 19
\(\seteqnumber{0}{}{63}\)\begin{equation*} h_{\mathrm {MCS}}(t) \lessapprox \lambda _{\mathrm {SENS\_ED.1}}\cdot Q_{\mathrm {SENS\_ED.2}}(t) + \lambda _{\mathrm {SENS\_ED.2}}\cdot Q_{\mathrm {SENS\_ED.1}}(t) \end{equation*}
Bei den Ereignissen SENS_ED.x wird nun auch die Nichtverfügbarkeit benötigt. Diese hängt gemäß Formel (48) im Allgemeinen von der Zeit zur Detektion und der Reparaturzeit ab. Da in diesen Ereignissen nur die Ausfälle betrachtet werden, die sofort erkennbar sind, wird die Detektionszeit zu null modelliert. Die Reparaturzeit ist die Zeit, für die der andere Sensor noch durchhalten muss, sei es bis ein sicherer Zustand erreicht ist (z. B. die Landung des Flugzeugs erfolgt ist), oder bis eine Reparatur bei laufendem Betrieb erfolgt ist. Sie ist hier mit 100 h angenommen.
Mit Formel (47) gilt
\(\seteqnumber{0}{}{63}\)\begin{equation*} \overline {Q} \approx \lambda \cdot \mathrm {MRT} = \SI {1e-4}{\per \hour } \cdot \SI {100}{\hour }= \num {0.01} \end{equation*}
und somit für den Minimalschnitt
\(\seteqnumber{0}{}{63}\)\begin{equation*} h_{\mathrm {MCS}}(t)=\overline {h_{\mathrm {MCS}}} =\SI {1e-4}{\per \hour }\cdot \num {0.01}+\SI {1e-4}{\per \hour }\cdot \num {0.01}=\SI {2e-6}{\per \hour } \end{equation*}
Da auch die Ausfallraten der anderen Minimalschnitte konstant sind, beträgt die Gesamt-Ausfallrate des Systems somit
\(\seteqnumber{0}{}{63}\)\begin{equation*} h_{\mathrm {sys}}=\SI {1e-6}{\per \hour }+\SI {1e-5}{\per \hour }+2\cdot \SI {1e-5}{\per \hour }+\SI {2e-6}{\per \hour }=\SI {3.3e-5}{\per \hour } \end{equation*}
-
19 bezüglich der Exaktheit siehe Kommentar zu Formel (64)
Die im Beispiel verwendete Formel für die Eintrittsrate eines Minimalschnitts lässt sich auf Minimalschnitte beliebiger Ordnung \(m=n_{\mathrm {Lit}}\) erweitern:
\(\seteqnumber{0}{}{63}\)\begin{equation} \label {eq:h_mcs} \begin{split} h_{\mathrm {MCS}}(t) & \lessapprox h_{1}(t) \cdot Q_{2}(t) \cdot Q_{3}(t) \cdot \ldots \cdot Q_{m}(t) \\ & + h_{2}(t) \cdot Q_{1}(t) \cdot Q_{3}(t) \cdot \ldots \cdot Q_{m}(t) \\ & + \dots \\ & + h_{m}(t) \cdot Q_{1}(t) \cdot Q_{2}(t) \cdot \ldots \cdot Q_{m-1}(t)\\ &=\sum _{j=1}^{m} \left ( h_j(t) \cdot \prod _{k=1,k\neq j}^{m} Q_{k}(t) \right ) \end {split} \end{equation}
Formel (64) ist nur für \(Q_i \rightarrow 0\) korrekt. Die exakte Formel für zwei Ereignisse mit beliebig großen Nichtverfügbarkeiten wird in Beispiel 6.7 hergeleitet. Der Fehler fällt jedoch erst für große Nichtverfügbarkeiten ins Gewicht, ist also für korrekt ausgelegte Systeme (also wenn die Detektions- und Reparaturzeiten wesentlich kleiner sind als die MTTF) unrelevant. Die Formel ist zudem immer konservativ, so dass selbst bei nicht korrekt ausgelegten Systemen die Ausfallrate nicht zu klein geschätzt wird.
Für die System-Ausfallrate (oder allgemeiner: die Eintrittsrate des Top-Events) gilt
\(\seteqnumber{0}{}{64}\)\begin{equation} \label {eq:h_sys_mcs} \begin{split} h_{\mathrm {sys}}(t) &\lessapprox h_{\mathrm {MCS 1}}(t) + h_{\mathrm {MCS 2}}(t) + \ldots + h_{\mathrm {MCS n}}(t)\\ &= \sum _{i=1}^{n_{\mathrm {MCS}}} \left ( \sum _{j=1}^{n_{\mathrm {Lit,MCS_i}}} \left ( h_j(t) \cdot \prod _{k=1,k\neq j}^{n_{\mathrm {Lit,MCS_i}}} q_{i,k}(t) \right ) \right ) \end {split} \end{equation}
Diese Formel gilt exakt nur, wenn alle Minimalschnitte nur aus einem Ereignis bestehen. Andernfalls kann es sein, dass sich die Minimalschnitte gegenseitig überlappen, so dass das Ergebnis etwas zu groß wird. Dies lässt sich wie bei der Berechnung der System-Nichtverfügbarkeit durch Disjunktion der Minimalschnitte berücksichtigen. Diese Operation ist jedoch sehr aufwändig und stößt selbst bei Verwendung von BDDs bei großen Fehlerbäumen an die Leistungsgrenzen moderner PCs.
6.1.3 Einkanalig Fail-Safe
Im letzten Beispiel wurde angenommen, dass der Prozess nicht einfach abgeschaltet und in einen sicheren Zustand gebracht werden kann, wenn ein Fehler erkannt wird. Bei vielen Prozessen ist dies durchaus möglich, beispielsweise kann ein Zug immer noch sicher zum Stillstand gebracht werden, wenn die Weg- oder Geschwindigkeitsmessung ausfällt. Dabei muss nicht einmal bekannt sein, welche Komponente genau ausgefallen ist, sondern man kann den sicheren Zustand auch im Fall von Inkonsistenzen jeglicher Art anfordern. Dies soll im nächsten Beispiel verdeutlicht werden.
Gelegentlich spricht man von einer Fail-Safe-Architektur, wenn die Steuerung in der Lage ist, den Prozess im Fall erkannter Fehler in einen sicheren Zustand zu bringen. Der Begriff ist allerdings äußerst unscharf, denn nirgends ist definiert, welche Fehlermodi oder welcher Anteil der gefährlichen Fehlermodi erkannt werden müssen, um ein System „fehlersicher“ nennen zu dürfen. 20
20 Eine vollständige Erkennung und Behandlung aller kritischen Fehler gilt gemeinhin als unmöglich.
-
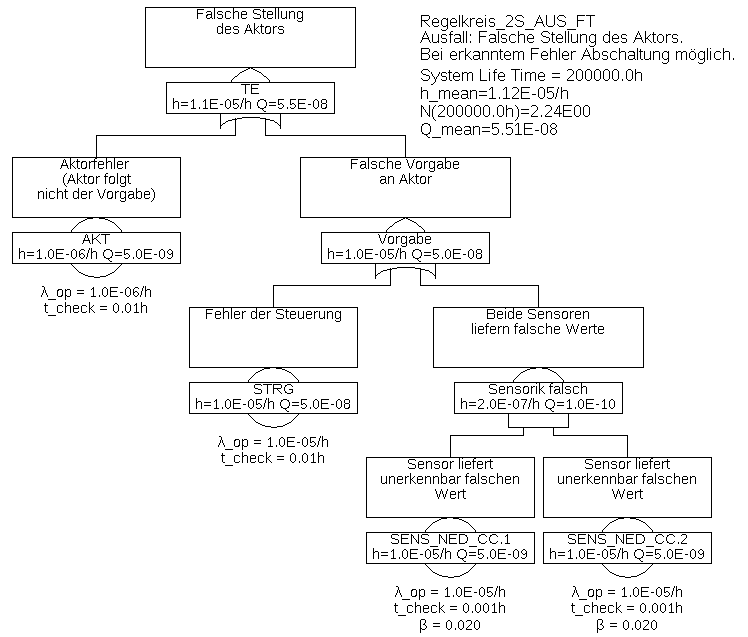
Beispiel 6.3 In diesem Beispiel wird angenommen, dass die Steuerung in dem Fall, dass sie einen Fehler erkennt, den Aktor so ansteuert, dass der Prozess in einen sicheren Zustand geht (beispielsweise Abschalten der Energiezufuhr oder Anlegen der Bremsen).
In diesem Fall sind die erkennbaren Ausfälle der Sensoren SENS_ED nicht mehr gefährlich und können somit ignoriert werden. Und auch der Zustand, dass ein Sensor falsche Werte liefert, jedoch nicht klar ist welcher, ist unkritisch, da im Fall einer Diskrepanz die Steuerung den Aktor ebenfalls so ansteuern wird, dass der Prozess einen sicheren Zustand erreicht.
Gefährlich ist nur der Fall, dass beide Sensoren gleichzeitig unerkennbar falsche Werte liefern, also die Ausfälle SENS_NED.1 und SENS_NED.2 gleichzeitig vorliegen, und die falschen Werte noch dazu so ähnlich sind, dass dies für die Steuerung nicht als Fehler erkennbar ist. Die beiden Ausfälle müssten also nicht nur im Detail ähnlich sein, sondern auch noch so schnell hintereinander passieren, dass dies für die Steuerung nicht sichtbar wäre, also typischerweise innerhalb der Prozessfehlertoleranzzeit (PFTZ). Man mag verleitet sein anzunehmen, dass so ein Fall praktisch nie eintreten wird. Tatsächlich wird dieser Fall wohl auch nicht durch unabhängige zufällige Ereignisse eintreten, die Erfahrung zeigt aber, dass es immer wieder zu gleichzeitigen Ausfällen redundanter Komponenten aufgrund nicht berücksichtigter äußerer Umstände kommt. Flug AF447 oder die Katastrophe von Fukushima sind bekannte Beispiele hierfür. Um die Realität möglichst korrekt zu modellieren, sollte man einen Faktor für den Anteil von gemeinsamen Ausfällen aufgrund nicht näher bekannter oder berücksichtigter äußerer Umstände annehmen. In [IEC 61508] wird dieser Common-Cause-Factor genannt und mit \(\beta \) bezeichnet. In [IEC 61508] sind auch Tabellen enthalten, die bei der Schätzung dieses Faktors hilfreich sein können. Abbildung 24 zeigt den so erstellen Fehlerbaum. Hier wurde \(\beta =2\%\) zwischen den Ereignissen SENS_NED.1 und SENS_NED.2 angenommen und diese daher in SENS_NED_CC umbenannt.
Die Minimalschnitte und deren Teil-Eintrittsraten sind in Tabelle 1 gelistet.
Tabelle 1: Minimalschnitte für Beispiel 6.3Minimalschnitt Eintrittsrate \(\overline {h}\) STRG 1,0E-05/h AKT 1,0E-06/h SENS_NED_CC.COM 2,0E-07/h SENS_NED_CC.1 & SENS_NED_CC.2 9,604E-14/h Darin bezeichnet SENS_NED_CC.COM das Common-Cause-Ereignis, dass beide Sensoren gleichzeitig (aufgrund eines gleichzeitig wirkenden äußeren Ereignisses) unerkennbar ausfallen. Seine Eintrittsrate beträgt \(\beta \cdot \lambda _{\mathrm {SENS\_NED\_CC}} = 0,02 \cdot \SI {1,0e-5}{\per \hour } = \SI {2,0e-7}{\per \hour }\).
Die Ausfallrate der Sensorik (Gatter „Sensorik falsch“) ändert sich damit von \(\SI {2.2e-5}{\per \hour }\) auf \(\SI {2.0e-7}{\per \hour }\). Die Sensorik hat in diesem Fall also keinen großen Anteil an der Gesamt-Ausfallrate mehr.
Allgemein gilt: Bei der Modellierung können Ausfälle, die unmittelbar zur sicheren Seite gehen, oder bei deren Eintritt eine immer zur Verfügung stehende Maßnahme mit höchster Wahrscheinlichkeit einen sicheren Zustand herbeiführt, weggelassen werden. Es muss jedoch unbedingt geprüft werden, ob diese Maßnahmen auch tatsächlich vorhanden und geeignet sind, in allen Fällen einen sicheren Zustand (des Prozesses!) zu erreichen. Um diese Prüfung durchführen zu können, müssen alle angenommenen Maßnahmen und sicheren Zustände zwingend erwähnt und insbesondere bei generischen Komponenten in die für den Kunden bestimmte Dokumentation des Produkts übernommen werden.
Bei Ereignissen unterhalb von UND-Gattern ist eine korrekte Modellierung der Nichtverfügbarkeit nötig. Diese basiert auf Fehlerdetektions- und Wiederherstellungszeiten. Zudem kann es notwendig sein, gleichzeitige Ausfälle redundanter Komponenten zu berücksichtigen, beispielsweise durch Common-Cause-Faktoren \(\beta \).
Zur korrekten Modellierung von Diagnose und Inspektion ist die Kenntniss des physikalischen oder technischen Prozesses, in den die Sicherheitsfunktion eingebettet ist notwenig. Ist diese (noch) nicht bekannt, müssen alle getroffenen Annahmen als Bedingungen bezüglich der Gültigkeit des Fehlerbaums dokumentiert und ggf. an Kunden weitergegeben werden.
6.1.4 Modellierung von regelmäßigen Tests und Diagnose
In Beispiel 6.3 wurde angenommen, dass sich der Prozess leicht in einen sicheren Zustand bringen lässt. Die Sicherheit ist maßgeblich durch die Ausfallrate der Steuerung bestimmt. Es liegt nun nahe, eine Diagnoseeinheit zu ergänzen, welche die Aktivität der Steuerung überwacht. Wenn die Diagnoseeinheit einen Fehler erkennt, bringt sie den Prozess (z. B. die Maschine oder die verfahrenstechnische Anlage) typischerweise über einen zusätzlichen, einfach aufgebauten binären Not-Aktor (beispielsweise ein Relais oder ein Abschaltventil) in einen sicheren Zustand (Stillstand, Leerlauf). Die Grundarchitektur solcher Steuerungen oder Regelungen ist in Abbildung 25 dargestellt. Sie wird oft als einkanalig mit Diagnose, kurz 1oo1D (für engl. 1-out-of-1) bezeichnet.
Die systematische Qualität der Diagnoseeinheit, also der Anteil der durch die Diagnose rechtzeitig erkennbaren Ausfälle an der Gesamtheit der (gefährlichen) Ausfallmodi des diagnostizierten Bauteils, wird als Diagnose-Deckungsgrad (engl. Diagnostic Coverage, DC) bezeichnet. Angenommen die Diagnoseeinheit überwacht die Versorgungsspannungen, den Prozessortakt und die regelmäßige Abarbeitung der kritischen Software-Tasks (Watchdog-Funktion), nicht jedoch die Logik der Recheneinheiten, die Speicher, oder die Ein-/Ausgabeeinheiten (A/D- und D/A-Wandler etc.) der Steuerung, so erhält man gemäß Tabellen in einschlägigen Normen vielleicht einen Diagnose-Deckungsgrad von 70%.
Es gibt nun mindestens drei Möglichkeiten, die Diagnose zu modellieren:
-
1. Man verringert die Ausfallrate der diagnostizierten Komponente (hier STRG) entsprechend des Diagnose-Deckungsgrads. Die Diagnose taucht also im Fehlerbaum nicht explizit auf. Der Vorteil ist offensichtlich ein einfacher Fehlerbaum. Nachteil ist, dass die Diagnose nicht ausdrücklich als sicherheitsrelevante Komponente erwähnt wird, man also stillschweigend voraussetzt, dass die Diagnose immer funktionieren wird. Tatsächlich aber unterliegt auch die Diagnose und insbesondere der Abschaltpfad zufälligen Ausfällen und muss daher in den meisten Anwendungen regelmäßig getestet werden.
-
2. Man teilt die Ausfälle der diagnostizierten Komponente gemäß Diagnose-Deckungsgrad auf zwei Basisereignisse auf, eines für die von der Diagnose nicht detektierbaren Ausfälle (AUSFALL_UNDET), eines für die detektierbaren (AUSFALL_DET).
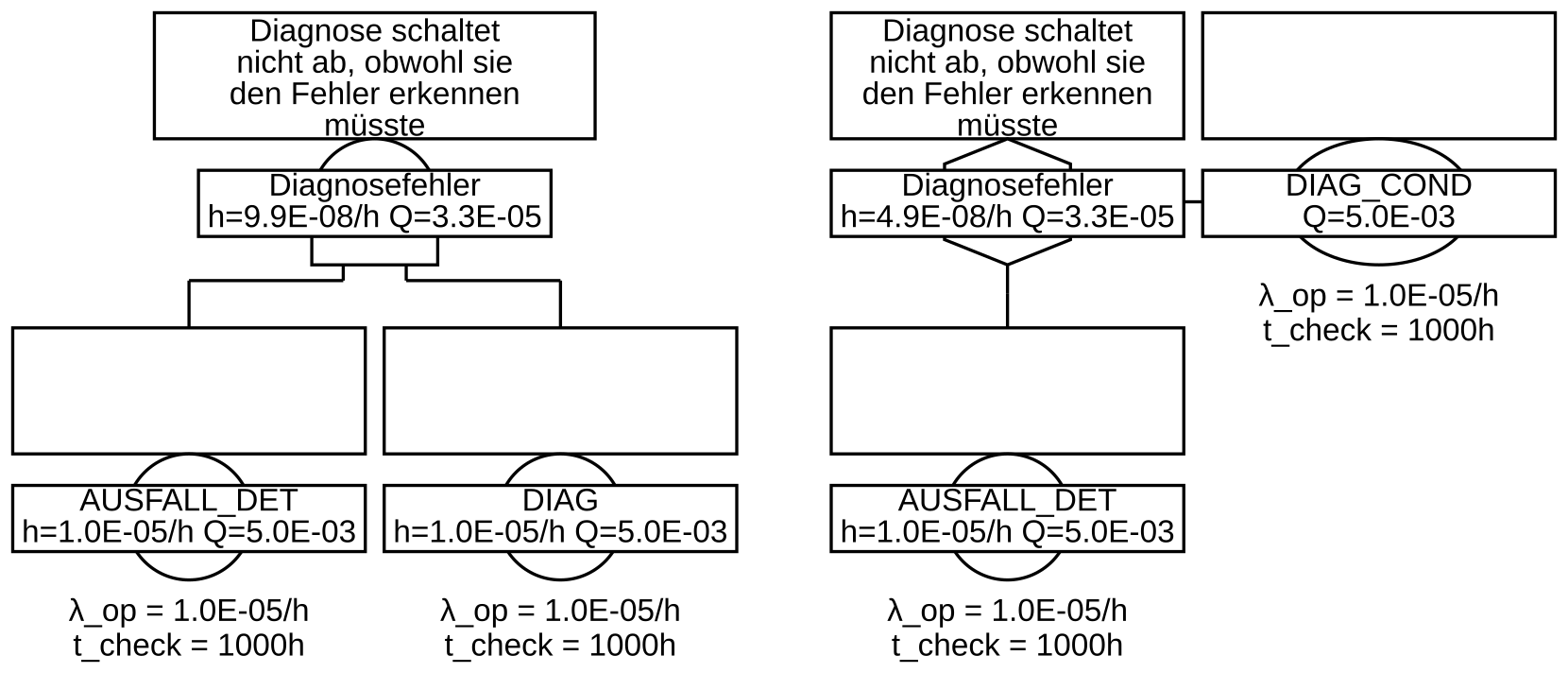
Der Ausfall der Diagnose selbst wird ebenfalls als Basisereignis (DIAG) mit einer bestimmten Ausfallrate und Testintervall modelliert. Das Ereignis für die erkennbaren Ausfälle wird mit der Diagnose mittels UND-Gatter verbunden, vgl. Abbildung 26 links.
-
3. Wie zuvor, aber das Basisereignis des Diagnoseausfalls wird als Bedingung (engl. Condition) gekennzeichnet (DIAG_COND), und mittels INHIBIT-Gatter mit dem zu diagnostizierenden Ausfall (AUSFALL_DET) verbunden, vgl. Abbildung 26 rechts.
Der Unterschied der Varianten 2 und 3 ist folgender: Beim UND-Gatter gilt Formel (64). Bei der Verknüpfung von AUSFALL_DET und DIAG ergibt sich also
\(\seteqnumber{0}{}{65}\)\begin{equation*} h_\mathrm {UND} = h_\mathrm {AUSFALL\_DET} \cdot Q_\mathrm {DIAG} + h_\mathrm {DIAG} \cdot Q_\mathrm {AUSFALL\_DET} \end{equation*}
Das spiegelt aber nicht die Realität wider, denn die Ausfallrate der Diagnose \(h_\mathrm {DIAG}\) hat keinerlei Einfluss auf die Eintrittsrate des Systemausfalls, sondern nur deren Nichtverfügbarkeit \(Q_\mathrm {DIAG}\). Solange also \(Q_\mathrm {DIAG}\) konstant ist, sollte auch die Ausfallrate der Verknüpfung gleich bleiben. Dies erreicht man, indem man ein Ereignis als Bedingung kennzeichnet, und mittels INHIBIT an die durch Eintrittsraten \(h\) und Nichtverfügbarkeiten \(Q\) beschriebenen „normalen“ Teile des Fehlerbaums anbindet. Damit wird die Eintrittsrate der Bedingung ignoriert (als wäre sie null), und somit wird der zweite Summand in vorheriger Formel null – genau das, was hier gewünscht ist:
\(\seteqnumber{0}{}{65}\)\begin{equation*} h_\mathrm {INHIBIT} = h_\mathrm {AUSFALL\_DET} \cdot Q_\mathrm {DIAG} + 0 \cdot Q_\mathrm {AUSFALL\_DET} \end{equation*}
Anmerkung: Die Unterscheidung von UND und INHIBIT mag in unterschiedlichen Werkzeugen unterschiedlich streng gehandhabt werden, da es auch hier keine Standardisierung gibt.
Anmerkung: Oft beschreibt man mit einem Bedingungs-Ereignis auch die Wahrscheinlichkeit, dass bestimmte Randbedingungen vorliegen. In dem Fall wird diese Wahrscheinlichkeit direkt als Konstante eingegeben, siehe Anhang A.3.
Anmerkung: Bedingungen können miteinander verknüpft werden (z. B. mittels UND-, oder ODER-Gattern), bevor sie als Gesamt-Bedingung an ein INHIBIT-Gatter angeschlossen werden.
-
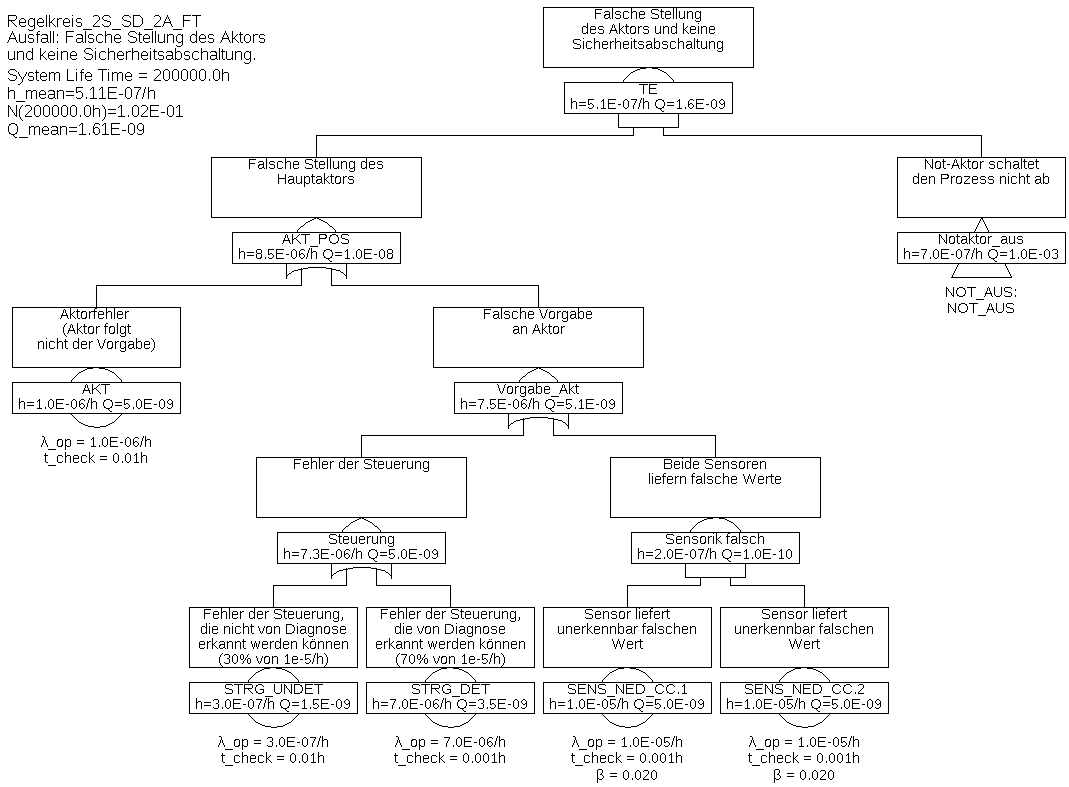
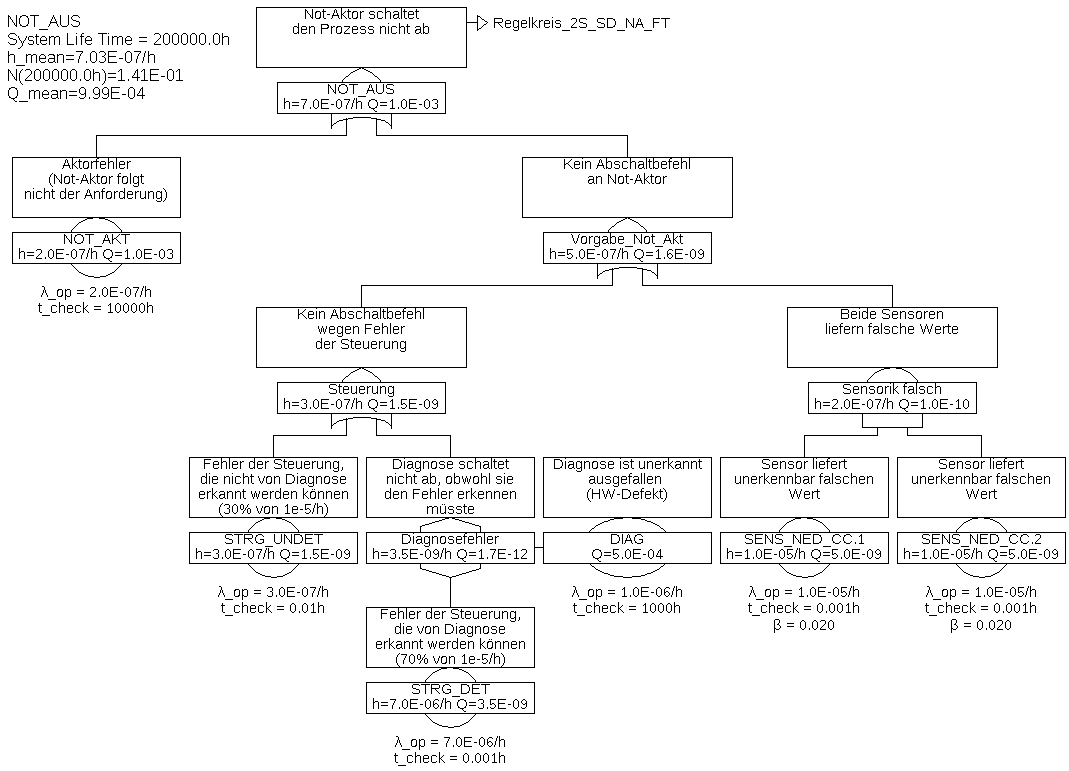
Beispiel 6.4 Die Abbildungen 27 und 28 stellen den Fehlerbaum für eine Architektur dar, in der die Steuerung diagnostiziert wird und im Falle eines erkennbaren Ausfalls der Prozess abgeschaltet wird.
Der Fehlerbaum wurde aus Platzgründen in zwei Teil-Fehlerbäume aufgeteilt. Der Teil-Baum für das Gatter „Notaktor_aus“ wurde mittels eines Transfer-Gatters mit dem übergeordneten Fehlerbaum verbunden. Das Transfer-Gatter selbst hat keinerlei Auswirkung auf die Berechnung, es ist nur ein Verweis auf einen Zweig an anderer Stelle.
Dabei wird angenommen, dass die Abschaltung über den Notaktor auch dann erfolgt, wenn die Steuerung erkennt, dass der Haupt-Aktor defekt ist. Dies ist in vielen Anwendungen leicht und rechtzeitig daran zu erkennen, dass die Regelgröße zunehmend vom Sollwert abweicht, oder die Steuerung liest die Stellgröße über einen zusätzlichen Sensor zurück. Einen Aktor-Fehler kann die Steuerung der Diagnose einfach dadurch melden, dass sie sich in einen von der Diagnose erkennbaren Fehlerzustand versetzt (z. B. einen Watchdog nicht mehr zurücksetzt).
Die Minimalschnitte sind in Tabelle 2 gelistet.
Tabelle 2: Minimalschnitte für Beispiel 6.4Minimalschnitt Eintrittsrate \(\overline {h}\) STRG_UNDET 3,0E-07/h SENS_NED_CC.COM 2,0E-07/h STRG_DET & NOT_AKT 6,988E-09/h STRG_DET & DIAG 3,495E-09/h AKT & NOT_AKT 9,983E-10/h SENS_NED_CC.1 & SENS_NED_CC.2 9,604E-14/h Sobald es Minimalschnitte mit mehr als einem Ereignis gibt, sind die Nichtverfügbarkeit der darin enthaltenen Ereignisse und somit über die Fehlerdetektions- und Reparaturzeiten wesentlich. Diese müssen daher korrekt gewählt und begründet werden, wie in Tabelle 3 dargestellt. Die Prozessfehlertoleranzzeit wurde mit 0,01 h angenommen.
Tabelle 3: Basisereignisse für Beispiel 6.4Ereignis Fehleroffenbarung
Fehleroffenbarungszeit STRG_UNDET Systemausfall, Einzelfehler
unrelevant STRG_DET Diagnose
0,001 h NOT_AKT jährlicher Test
ca. 10000 h DIAG Einschalt-Selbsttest nach monatlicher Wartung/Reinigung
ca. 1000 h AKT Steuerung (unerwartetes Prozessverhalten)
0,01 h SENS_NED_CC a) Differenz der Sensoren
unmittelbar (0,001 h) SENS_NED_CC b) Gleichzeitiger Ausfall beider Sensoren:
über Common-Cause \(\beta \) berücksichtigt, Einzelfehlerunrelevant Die Eintrittsrate gefährlicher Ausfälle des Systems beträgt nun also nur noch 5,1E-7/h und wird maßgeblich von den unerkannten Fehlern der Steuerung bestimmt. Weitere Verbesserungen könnten durch Einsatz spezieller Sicherheitsprozessoren (beispielsweise Dual-Core Prozessoren im Lock-Step) und spezieller Speicher (ECC) erreicht werden.
6.1.5 Zweikanalig Fail-Safe
Das in Beispiel 6.4 betrachtet System wird gelegentlich als fehlersicheres einkanaliges System mit Diagnose (1oo1D) bezeichnet.
Steuerungen für hohe Sicherheitsanforderungen baut man oft aus zwei gleichartigen Einzelsteuerungen auf, wovon jede mit einer eigenen Diagnose versehen ist. Ist jede der Steuerungen in der Lage, den Prozess im Fall erkannter Fehler in einen sicheren Zustand zu bringen, wird dies manchmal als zweikanaliges fehlersicheres System, oder 1-aus-2 System mit Diagnose bezeichnet, kurz 1oo2D. Man sollte diese Bezeichnungen aber nur mit Vorsicht verwenden, da sie nicht harmonisiert sind, und in der Literatur durchaus unterschiedlich und sogar widersprüchlich verwendet werden. 21
21 In [IEC 61508] wird diese Architektur mit 1oo2 statt 1oo2D bezeichnet, da gemäß dieser Norm immer eine Diagnose vorhanden sein muss. In Teil 6 der Norm wird mit 1oo2D eine Art Fail-Operational Architektur bezeichnet, was sehr unüblich ist und daher oft missverstanden wird, zumal der Begleittext dies nicht klar erläutert.
-
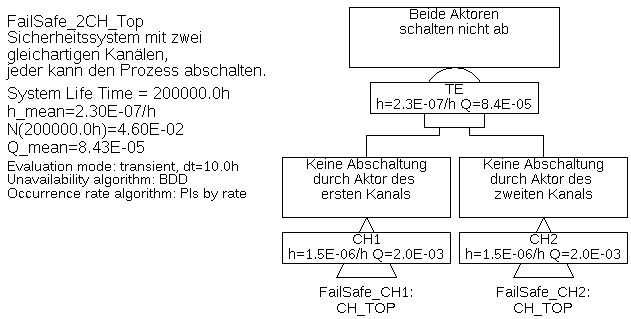
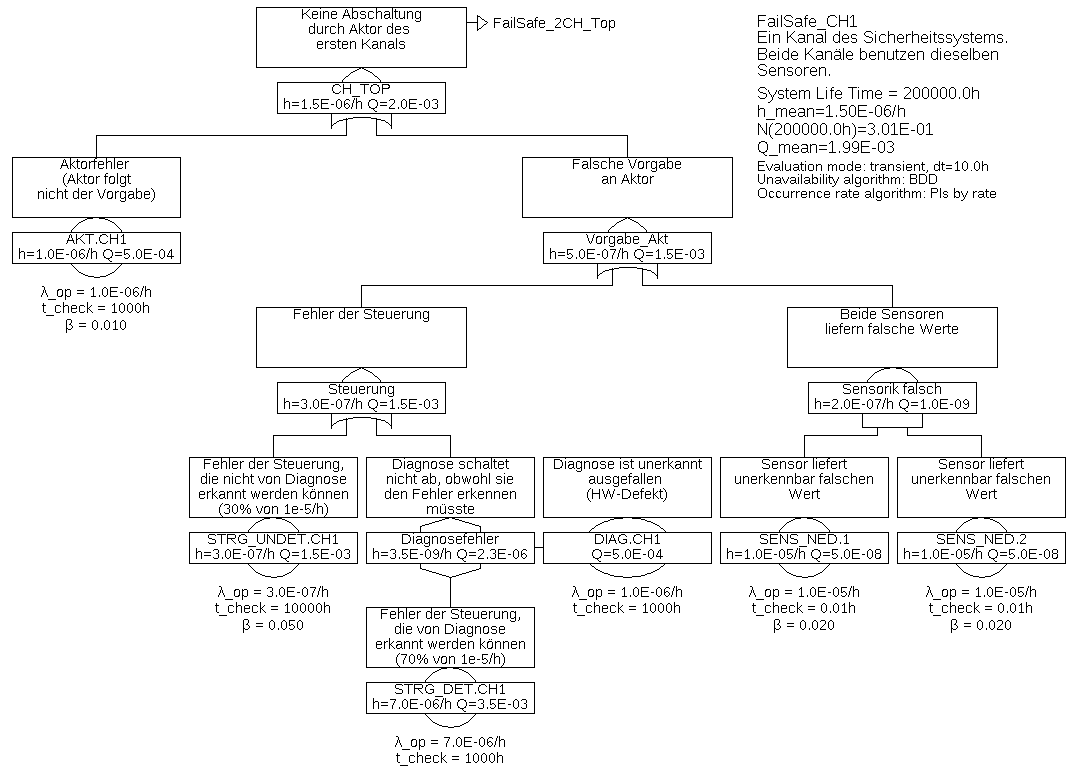
Beispiel 6.5 Der Fehlerbaum eines zweikanaligen Steuerungssystems, bestehend aus der von den vorherigen Beispielen schon bekannten Sensorik, welche gemeinsam von zwei Steuerungen mit jeweils eigener Diagnose und eigenem Aktor verwendet wird, ist in Abbildung 29 mit dem unterlagerten Baum gemäß Abbildung 30 dargestellt. Da die Kanäle gleich aufgebaut sind, ist nur der Teil-Fehlerbaum des ersten Kanals dargestellt.
Jede Steuerung kann bei erkannten Fehlern den Prozess über ihren Aktor in einen sicheren Zustand versetzen, auch die Diagnoseeinheit dieses Kanals nutzt den Aktor hierfür. Zumindest für undetektierbare Ausfälle von Sensorik und Elektronik, sowie Ausfälle von Aktoren kann man Ausfälle aufgrund gemeinsamer Ursachen meist nicht ausschließen. Daher wurden hier nicht nur (wie bisher) die unerkennbaren Ausfälle der Sensoren, sondern auch die unerkennbaren Ausfälle der Steuerungen und die Ausfälle der Aktoren mit Common-Cause-Faktoren versehen.
Für das System können die in Tabelle 4 gelisteten Minimalschnitte ermittelt werden.
Tabelle 4: Minimalschnitte für Beispiel 6.5Minimalschnitt Eintrittsrate \(\overline {h}\) SENS_NED.COM 2,0E-07/h STRG_UNDET.COM 1,5E-08/h AKT.COM 1,0E-08/h AKT.CH1 & STRG_UNDET.CH2 1,548E-09/h AKT.CH2 & STRG_UNDET.CH1 1,548E-09/h AKT.CH1 & AKT.CH2 9,699E-10/h STRG_UNDET.CH1 & STRG_UNDET.CH2 8,106E-10/h STRG_DET.CH2 & STRG_UNDET.CH1 & DIAG.CH2 5,745E-12/h STRG_DET.CH1 & STRG_UNDET.CH2 & DIAG.CH1 5,745E-12/h AKT.CH1 & STRG_DET.CH2 & DIAG.CH2 4,542E-12/h AKT.CH2 & STRG_DET.CH1 & DIAG.CH1 4,542E-12/h SENS_NED.1 & SENS_NED.2 9,604E-13/h STRG_DET.CH1 & DIAG.CH1 & STRG_DET.CH2 & DIAG.CH2 2,393E-14/h Aus Tabelle 4 geht deutlich hervor, dass die Ausfälle aufgrund gemeinsamer Ursache die wesentlichen Ereignisse sind. Das ist nicht nur in diesem Beispiel so, sondern entspricht der praktischen Erfahrung. Aus diesem Grund muss bei mehrkanaligen Systemen immer eine Common-Cause-Analyse durchgeführt werde, und eine Vielzahl von Maßnahmen ergriffen werden, um die Rate von Ausfällen aufgrund gemeinsamer Ursache (mathematisch beschrieben durch den \(\beta \)-Faktor) möglichst klein zu halten.
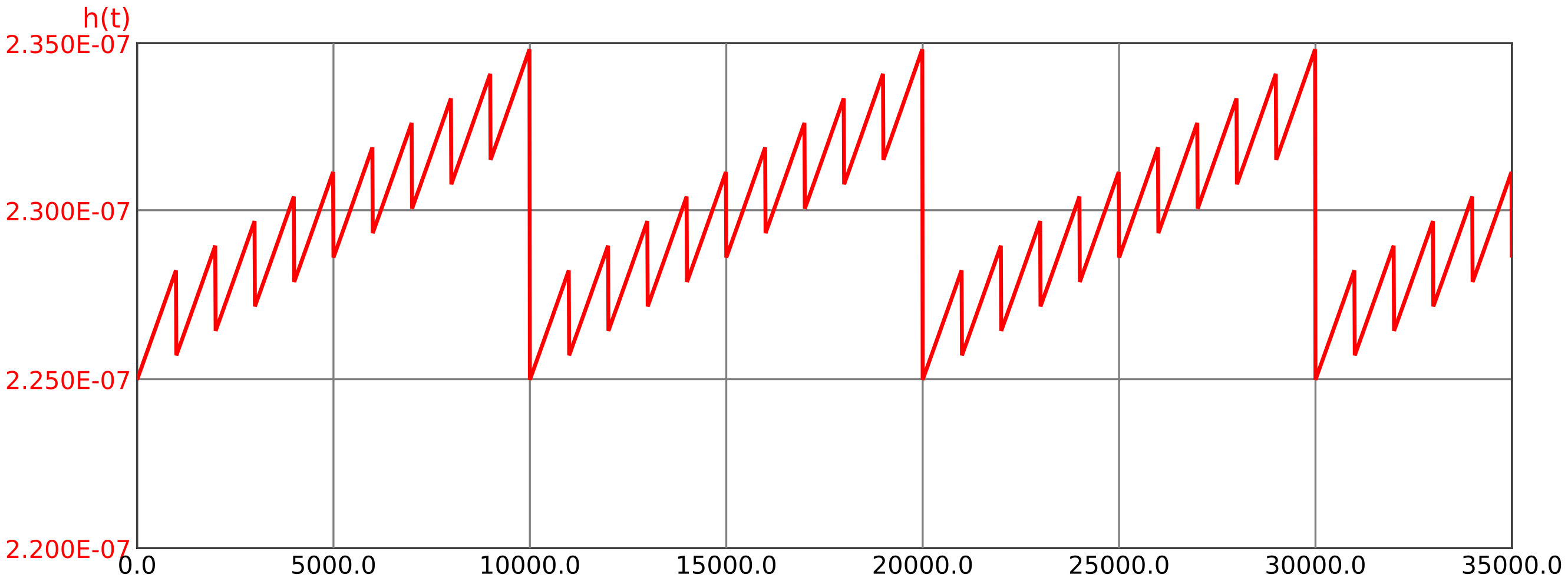
Der Verlauf der Ausfallrate über der Zeit ist in Abbildung 31 dargestellt.
Auf den ersten Blick mag verwundern, dass die Ausfallrate des Systems nicht konstant ist, obwohl doch die Ausfallraten aller Komponenten konstant sind. Dies liegt an der zeitvarianten Nichtverfügbarkeit jedes Kanals, welche gemäß Formel (64) in die Ausfallrate eingeht. Aufgrund der hohen Common-Cause-Anteile (siehe Minimalschnitte in Tabelle 4), welche direkt – ohne Multiplikation mit einer Nichtverfügbarkeit – in die System-Ausfallrate eingehen, ist die Zeitabhängigkeit allerdings nur gering (man beachte die Skala für \(h(t)\) in Abbildung 31).
6.1.6 Fail-Operational Systeme
Wie im einleitenden Beispiel 6.1 erwähnt, gibt es eine Vielzahl von Prozessen, die sich nicht einfach in einen sicheren Zustand bringen lassen.
Falls die Sicherheitsanforderungen nicht sehr hoch sind, genügt oft eine zweikanalige Architektur, wobei im Falle eines erkannten Fehlers jeder Kanal sich selbst abschalten kann oder sich gegenüber einer Auswahlschaltung als defekt erklären kann. Eine gute Eigendiagnose jedes einzelnen Kanals ist hierfür unerlässlich, denn nur wenn klar ist, welcher Kanal defekt ist, kann auf den intakten Kanal umgeschaltet werden. Die Umschaltung selbst muss durch eine nachgeschaltete Auswahlschaltung erfolgen.
Für höhere Sicherheitsanforderungen ist der Diagnose-Deckungsgrad der Kanal-internen Diagnose der einzelnen Kanäle oft nicht ausreichend, es kommt also zu einer zu großen Rate von widersprüchlichen Ausgaben der einzelnen Kanäle, ohne dass ein Kanal anzeigt, dass er defekt ist. Die Auswahlschaltung hätte in diesem Fall eine 50% Chance, den richtigen auszuwählen. Die Wahrscheinlichkeit, den richtigen Kanal abzuschalten, lässt sich dadurch wesentlich verbessern, dass die Ausgaben von drei Kanälen verglichen werden. Unter der Bedingung, dass systematische Fehler und Ausfälle aufgrund gemeinsamer Ursache hinreichend selten sind, werden in der Regel mindestens zwei Kanäle die korrekte Ausgangsgröße ermitteln. Die Auswahlschaltung wird daher so aufgebaut, dass sie die Ergebnisse der beiden Kanäle verwendet, deren Ergebnisse identisch sind oder zumindest am nähesten beieinander liegen. Eine solche Architektur wird als 2-aus-3-Architektur (2oo3 oder auch 2oo3D, falls jeder Kanal eine eigene Diagnose hat) bezeichnet. 22
Unabhängig von der Anzahl der Kanäle darf die Auswahlschaltung nur eine minimale Ausfallrate haben, um nicht das für die Gesamt-Sicherheit maßgebliche Element zu sein. Manchmal erfolgt die Auswahl auch über die Mechanik, beispielsweise in dem jeder von drei Kanälen einen Aktor treibt, welcher von zwei anderen mechanisch überstimmt werden kann. Bei entsprechender „Intelligenz“ der Auswahlschaltung kann ein 2oo3-System sogar mit zwei ausgefallenen Kanälen noch korrekt arbeiten, wenn die Ausfälle von der Kanal-Diagnose erkannt und an die Auswahllogik gemeldet werden.
22 Im Gegensatz zu 1oo2, 2oo2, 1oo3, 3oo3 ist bei 2oo3 eine Verwechslung nicht möglich, da jede Sichtweise dasselbe Ergebnis liefert.
-
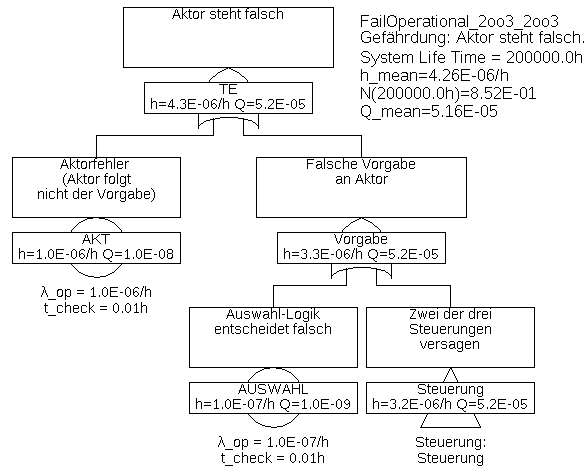
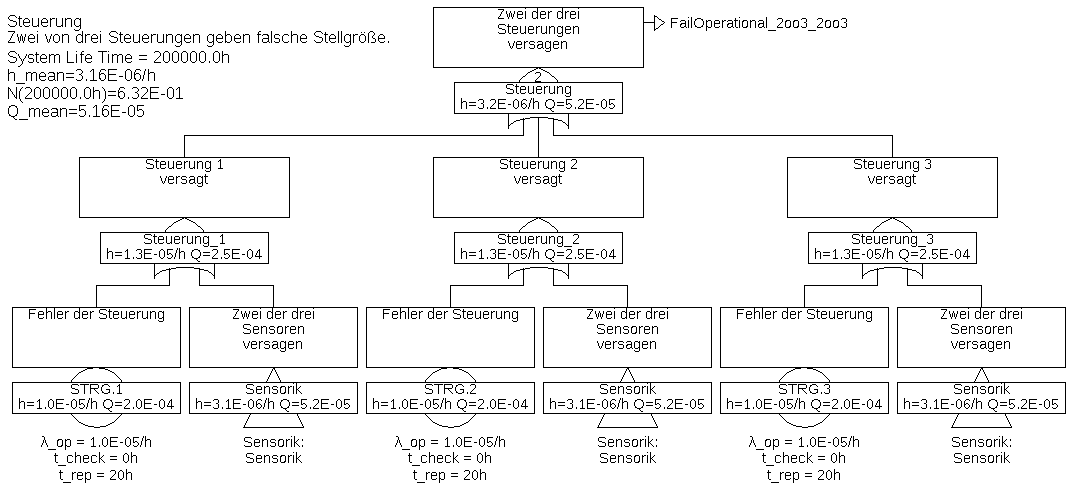
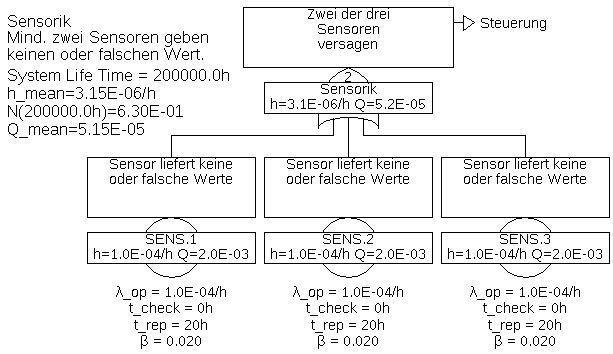
Beispiel 6.6 Dieses Beispiel verwendet die Komponenten des Beispiels 6.1 wieder. Allerdings werden nun drei Sensoren und drei Steuerungen (Rechner) eingesetzt, und zwar so, dass jede der Steuerungen die Werte aller drei Sensoren bekommt. Beim Ausfall eines Sensors können also alle drei Steuerungen weiterarbeiten, im Gegensatz zu einer Architektur, bei der jede Steuerung nur auf einen Sensor Zugriff hätte. Zudem kann so jede Steuerung Fehler der Sensorik erkennen. Die von den drei Steuerungen berechneten Vorgaben für den einzigen Aktor werden von einer Auswahl-Logik verglichen und gemäß Mehrheitsentscheidung (2-von-3) ausgewählt.
Der Fehlerbaum ist in Abbildung 32 dargestellt, mit den Unterbäumen in 33 und 34.
Die Gatter „Steuerung“ in Abbildung 33 und „Sensorik“ in Abbildung 34 sind Kombinations-Gatter, sie werden weiter unten erklärt.
Neben den Ausfallraten aller Komponenten sind die Nichtverfügbarkeiten der Steuerungen und der Sensoren relevant. Hier wurde angenommen, dass sich alle Ausfälle der Steuerungen sowie alle unabhängigen Ausfälle der Sensoren sofort durch Diskrepanzen in der Auswahl-Einheit offenbaren, die Detektionszeit \(t_\mathrm {check}\) also null ist. Die Zeit bis zur Reparatur, also die Zeit, die die verbliebenen Kanäle durchhalten müssen, wurde mit 20 h angenommen (man denke etwa an ein Langstreckenflugzeug, welches erst nach der Landung repariert werden kann, oder an ein Schiff, bei dem die Reparatur eines Aggregats zwar auf See erfolgt, aber eine Weile dauert).
Die Minimalschnitte sind in Tabelle 5 gelistet.
Tabelle 5: Minimalschnitte für Beispiel 6.6Minimalschnitt Eintrittsrate \(\overline {h}\) SENS.COM 2,0E-06/h AKT 1,0E-06/h SENS.1 & SENS.2 3,842E-07/h SENS.1 & SENS.3 3,842E-07/h SENS.2 & SENS.3 3,842E-07/h AUSWAHL 1,0E-07/h STRG.1 & STRG.2 4,0E-09/h STRG.1 & STRG.3 4,0E-09/h STRG.2 & STRG.3 4,0E-09/h Die Gesamt-Ausfallrate ist im Vergleich zum Beispiel 6.1 von 1,11E-4/h auf 4,26E-6/h gesunken, und wird nun hauptsächlich durch die Ausfälle der Sensoren aufgrund gemeinsamer Ursache (\(\beta \) wurde mit 2% angenommen) bestimmt.
Im vorherigen Beispiel wurden sogenannte KOMBINATIONS-Gatter (engl. Combination-Gate), auch Mehrheitsentscheider (engl. Voting-Gate) genannt, für die Gatter „Steuerung“ und „Sensorik“ verwendet. Sie sind nur eine Abkürzung für die entsprechende Kombination aus UND- und ODER-Gattern. Die Zahl im Gatter (oft mit \(m\) abgekürzt, hier also \(m=2\)) gibt an, wieviele der \(n\) Eingänge mindestens versagen müssen (also erfüllt sein müssen), damit das durch das Gatter beschriebene Ereignis eintritt. \(m=1\) bedeutet also ein reines ODER-Gatter, \(m=n\) bedeutet ein reines UND-Gatter, \(1<m<n\) bedeutet eine Kombination eines ODER- mit mehreren UND-Gattern, wie in Abbildung 35 beispielhaft für ein 2-von-3-Gatter gezeigt.
Zur Berechnung werden die Kombinations-Gatter in die entsprechende Kombination von UND- und ODER-Gattern umgewandelt. Es gibt daher keine besonderen Formeln oder Berechnungsmethoden für diese Gatter.
6.1.7 Transiente und stationäre Berechnung
Wie die mittlere System-Nichtverfügbarkeit kann auch die mittlere System-Ausfallrate sowohl über eine stationäre Berechnung als auch eine transiente Berechung ermittelt werden, siehe hierzu Abschnitt 5.1.4.
Einziger Unterschied ist, dass der in Abschnitt 5.1.4 beschriebene mathematische Fehler beim Rechnen mit Mittelwerten für die Ausfallrate erst bei Minimalschnitten dritter Ordnung (also Minimalschnitten mit drei Basis-Ereignissen) auftritt, und nicht schon bei Minimalschnitten zweiter Ordnung wie bei der Nichtverfügbarkeit. Das liegt daran, dass gemäß Formel (64) bei einem Minimalschnitt zweiter Ordnung noch keine Multiplikation von Nichtverfügbarkeiten auftritt. Wenn also klar ist, dass sich das System (abgesehen von einer im Vergleich zur Einsatzzeit vernachlässigbaren Einschwingphase) in einem quasi-stationären Zustand befinden wird, kann die System-Ausfallrate meist in guter Näherung mit Mittelwerten berechnet werden.
6.2 Berechnung mit Markov-Modellen
Bezüglich der Modellierung gibt es keine Unterschiede zu Kapitel 5.2.
Wie für die Berechnung der Nichtverfügbarkeit muss zunächst entweder der stationäre Zustand berechnet werden, oder das lineare Differenzialgleichungssystem muss über die Lebenszeit integriert werden.
Die Eintrittshäufigkeit \(w_i(t)\) eines Zustands \(i\) ist die Summe der \(m\) Transitionsraten \(h_{i,j}\), die zu diesem Zustand führen, jeweils multipliziert mit der Aufenthaltswahrscheinlichkeit im Ursprungszustand der jeweiligen Kante \(p_{\mathrm {ursprung}_{i,j}}\):
\(\seteqnumber{0}{}{65}\)\begin{equation} w_i(t) = \sum _{j=1}^m h_{\mathrm {ein}_{i,j}}(t) \cdot p_{\mathrm {ursprung}_{i,j}}(t) \label {eq:w_state} \end{equation}
Die System-Ausfallhäufigkeit ergibt sich aus der Summe der Zustands-Eintrittshäufigkeiten für alle \(n\) Ausfallzustände
\(\seteqnumber{0}{}{66}\)\begin{equation} w_\mathrm {sys}(t) = \sum _{i=1}^n w_i(t) = \sum _{i=1}^n \sum _{j=1}^m h_{\mathrm {ein}_{i,j}}(t) \cdot p_{\mathrm {ursprung}_{i,j}}(t) \label {eq:w_sys} \end{equation}
Die Ausfallhäufigkeit \(w(t)\) ist nur dann identisch zur gesuchten Ausfallrate \(h(t)\), wenn die Aufenthaltswahrscheinlichkeit in allen Ausfallzuständen null ist, da in der Praxis im Fall einer (quasi-)kontinuierlich benötigten Sicherheitsfunktion ein Systemausfall praktisch sofort erkannt wird (nämlich durch das Eintreten eines Unfalls), was zur unmittelbaren Beendigung des Betriebs führt. Der Betrieb wird erst nach der Reparatur oder dem Ersatz des Systems durch ein anderes oder neues wieder aufgenommen, die Zeit bis dahin darf zur Berechnung der Ausfallrate nicht berücksichtigt werden (sonst würde sie zu optimistisch, wie man sich leicht mit Extrem-Beispielen vor Augen führen kann).
Möchte man also ein Markov-Modell zur Berechnung der Ausfallrate \(h_\mathrm {sys}(t)\) bzw. \(\overline {h_\mathrm {sys}}\) einsetzen, muss man entweder von allen Ausfallzuständen eine Transition mit einer sehr hohen Rate \(\mu \) zurück in einen Nicht-Ausfallzustand modellieren (in der Regel zurück in den Ausgangszustand), oder man muss die Ausfallhäufigkeit \(w(t)\) durch die Wahrscheinlichkeit, nicht in einem Ausfallzustand zu sein, dividieren:
\(\seteqnumber{0}{}{67}\)\begin{equation} \label {eq:h_sys_MM} h_\mathrm {sys}(t) = \frac {w_\mathrm {sys}(t)}{1-\sum \limits _{i=1}^n p_i(t)} \end{equation}
Falls die Wahrscheinlichkeiten der Ausfallzustände null sind, ergibt sich \(h(t) = w(t)\). Formel (68) kann man und sollte man sicherheitshalber immer anwenden, auch wenn – wie zuvor erwähnt – bereits Transitionen mit großer Wiederherstellungsrate \(\mu \) im Modell eingefügt wurden.
-
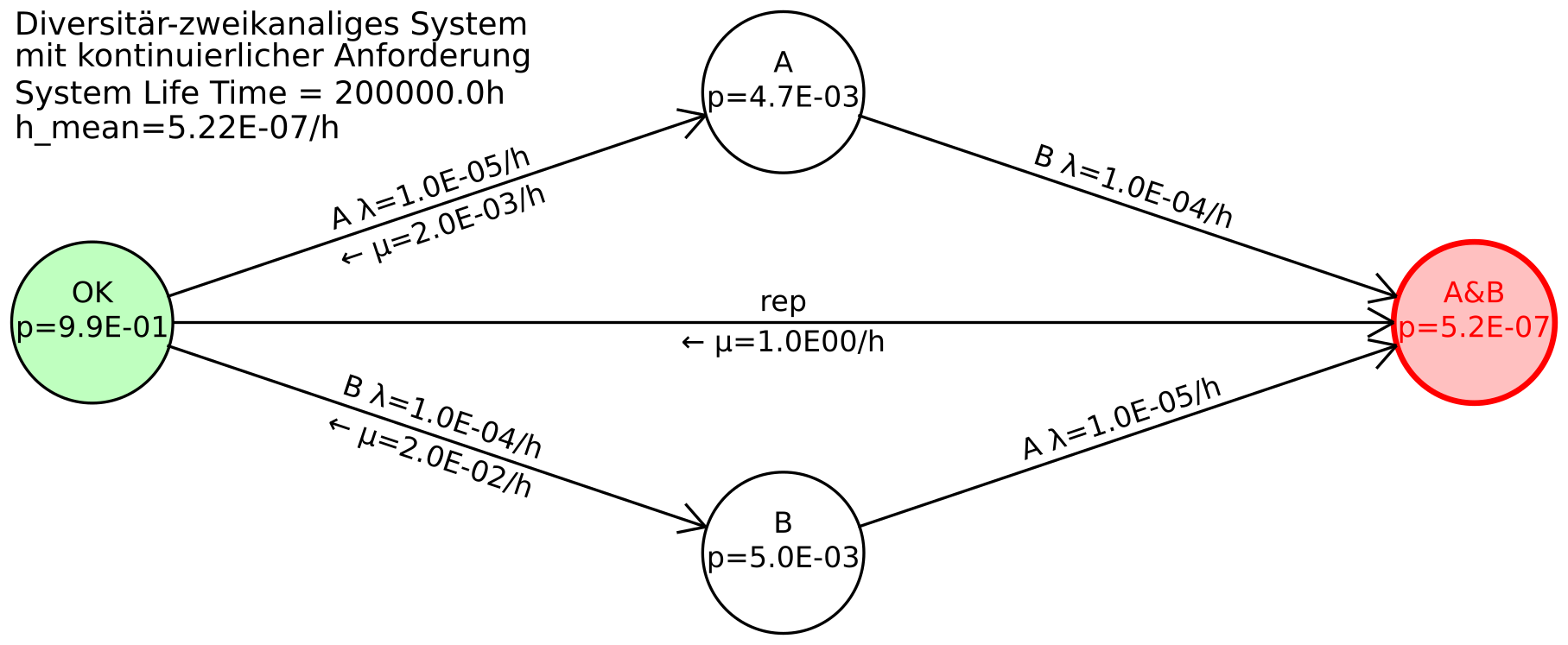
Beispiel 6.7 Die genannten Formeln sollen nun auf ein einfaches Markov-Modell angewandt werden. Hierfür wird ein einfaches diversitär-zweikanaliges System angenommen, bestehend aus den unterschiedlich aufgebauten (diversitären) Kanälen A und B. Die Kanäle A und B haben daher unterschiedliche Ausfallraten \(\lambda _\mathrm {A}\) und \(\lambda _\mathrm {B}\). Beide Kanäle A und B werden regelmäßig getestet, jedoch in unterschiedlichen Intervallen \(T_\mathrm {A}\) und \(T_\mathrm {B}\). Daraus ergeben sich unterschiedliche \(\mu _A=2/T_\mathrm {A}\) und \(\mu _B=2/T_\mathrm {B}\).
Wenn beide Kanäle versagen, versagt die kontinuierlich benötigte Sicherheitsfunktion, beendet also ihren Betrieb durch einen Unfall. Die Reparatur oder das Ersetzen des Systems nach einem Unfall führt zurück in den Ursprungszustand OK. Die Aufenthaltswahrscheinlichkeit im Zustand A&B während des Betriebs ist null, was durch ein im Vergleich zu den Ausfallraten sehr großes \(\mu _\mathrm {rep}\) modelliert wird.
Das zugehörige Markov-Modell ist in Abbildung 36 gezeigt.
Die Transitionsmatrix lautet:
\(\seteqnumber{0}{}{68}\)\begin{equation*} \label {T} T = \begin{pmatrix} -\lambda _A-\lambda _B & \mu _A & \mu _B & \mu _\mathrm {rep}\\ \lambda _A & -\mu _A-\lambda _B & 0 & 0\\ \lambda _B & 0 & -\mu _B-\lambda _A & 0\\ 0 & \lambda _B & \lambda _A & -\mu _\mathrm {rep} \end {pmatrix} \end{equation*}
Für die stationäre Berechnung wird eine der Zeilen zu 1 gesetzt (hier wurde die letzte genommen):
\(\seteqnumber{0}{}{68}\)\begin{equation*} \begin{pmatrix} -\lambda _B-\lambda _A & \mu _A & \mu _B & \mu _\mathrm {rep} \\ \lambda _A & -\mu _A-\lambda _B & 0 & 0 \\ \lambda _B & 0 & -\mu _B-\lambda _A & 0 \\ 1 & 1 & 1 & 1 \end {pmatrix} \cdot \vec {p}(t) = \begin{pmatrix} 0 \\ 0 \\ 0 \\ 1 \end {pmatrix} \end{equation*}
Die System-Eintrittsrate ergibt sich gemäß Formeln (67) und (68) zu
\(\seteqnumber{0}{}{68}\)\begin{equation*} h_\mathrm {sys} = \frac {p_\mathrm {A}\cdot \lambda _\mathrm {B}+p_\mathrm {B}\cdot \lambda _\mathrm {A}}{1-p_\mathrm {A\&B}} \end{equation*}
Die in dieser Formel benötigten Zustandswahrscheinlichkeiten \(p_\mathrm {A}\), \(p_\mathrm {B}\) und \(p_\mathrm {A\&B}\) werden durch Lösen des Gleichungssystems ermittelt. Damit ergibt sich \(h_\mathrm {sys}\) zu
\(\seteqnumber{0}{}{68}\)\begin{align*} h_\mathrm {sys} &= \dfrac {\lambda _{\mathrm {A}}\lambda _{\mathrm {B}}^{2} + \lambda _{\mathrm {A}}^{2}\lambda _{\mathrm {B}} +\lambda _{\mathrm {A}}\lambda _{\mathrm {B}}\mu _{\mathrm {A}} +\lambda _{\mathrm {A}}\lambda _{\mathrm {B}}\mu _{\mathrm {B}} } {\lambda _{\mathrm {A}}^{2}+\lambda _{\mathrm {B}}^{2}+\lambda _{\mathrm {A}}\lambda _{\mathrm {B}} +\left ( \lambda _{\mathrm {a}}+\lambda _{\mathrm {B}} \right ) \mu _{\mathrm {A}} +\left ( \lambda _{\mathrm {A}}+\lambda _{\mathrm {B}} \right ) \mu _{\mathrm {B}} +\mu _{\mathrm {A}} \mu _{\mathrm {B}} } \\ &= \dfrac { \lambda _{\mathrm {A}}\lambda _{\mathrm {B}} \left ( \lambda _{\mathrm {A}} + \lambda _{\mathrm {B}} + \mu _{\mathrm {A}} + \mu _{\mathrm {B}} \right ) } { \lambda _{\mathrm {A}} \left ( \lambda _{\mathrm {A}} + \mu _{\mathrm {A}} + \mu _{\mathrm {B}} \right ) + \lambda _{\mathrm {B}} \left ( \lambda _{\mathrm {B}} + \mu _{\mathrm {A}} + \mu _{\mathrm {B}} \right ) + \lambda _{\mathrm {A}}\lambda _{\mathrm {B}} + \mu _{\mathrm {A}} \mu _{\mathrm {B}} } \end{align*} Es sei bemerkt, dass die Rate \(\mu _\mathrm {rep}\) im Ergebnis nicht mehr auftaucht, da sie durch Formel (68) herausgekürzt wird. Dies entspricht genau der Erwartung, dass der Zahlenwert dieser Rate unrelevant sein muss. Diese Formel gilt nun für beliebige Testintervalle, im Gegensatz zu Formel (64), welche nur für ausreichend kleine Testintervalle gilt (andernfalls wird Formel (64) etwas zu groß).
Für geeignete Testintervalle \(T_{\mathrm {Test,A}} \ll 1/\lambda _{\mathrm {A}}\) und \(T_{\mathrm {Test,B}} \ll 1/\lambda _{\mathrm {B}}\) kann man \(\lambda _{\mathrm {A}}\) gegenüber \(\mu _{\mathrm {A}}\) und \(\lambda _{\mathrm {B}}\) gegenüber \(\mu _{\mathrm {B}}\) vernachlässigen und erst recht \(\lambda _{\mathrm {A}}\lambda _{\mathrm {B}}\) gegenüber \(\mu _{\mathrm {A}} \mu _{\mathrm {B}}\). Damit gilt näherungsweise:
\(\seteqnumber{0}{}{68}\)\begin{align*} h_\mathrm {sys} &\lessapprox \dfrac { \lambda _{\mathrm {A}}\lambda _{\mathrm {B}} \left ( \mu _\mathrm {A} + \mu _{\mathrm {B}} \right ) } { \lambda _{\mathrm {A}} \left ( \mu _\mathrm {A} + \mu _{\mathrm {B}} \right ) + \lambda _{\mathrm {B}} \left ( \mu _\mathrm {A} + \mu _{\mathrm {B}} \right ) + \mu _\mathrm {A} \mu _{\mathrm {B}} } \\ &= \dfrac { \lambda _{\mathrm {A}}\lambda _{\mathrm {B}} \left ( \dfrac {1}{\mu _\mathrm {A}} + \dfrac {1}{\mu _{\mathrm {B}}} \right ) } { \lambda _{\mathrm {A}} \left ( \dfrac {1}{\mu _\mathrm {A}} + \dfrac {1}{\mu _{\mathrm {B}}} \right ) + \lambda _{\mathrm {B}} \left ( \dfrac {1}{\mu _\mathrm {A}} + \dfrac {1}{\mu _{\mathrm {B}}} \right ) + 1 } \end{align*}
Unter derselben Bedingung (geeignete Testintervalle) gilt auch \(\lambda _{\mathrm {A}}/\mu _{\mathrm {A}} \ll 1\) und \(\lambda _{\mathrm {B}}/\mu _{\mathrm {B}} \ll 1\) und folglich die Näherung
\(\seteqnumber{0}{}{68}\)\begin{align*} h_\mathrm {sys} &\lessapprox \dfrac { \lambda _{\mathrm {A}}\lambda _{\mathrm {B}} \left ( \dfrac {1}{\mu _\mathrm {A}} + \dfrac {1}{\mu _{\mathrm {B}}} \right ) } { \dfrac {\lambda _{\mathrm {A}}}{\mu _{\mathrm {B}}} + \dfrac {\lambda _{\mathrm {B}}}{\mu _{\mathrm {A}}} + 1 } \end{align*}
Ersetzt man nun die Reparaturraten durch die Testintervalle durch \(\mu _\mathrm {i} \approx 2/T_{\mathrm {Test,i}}\), so erhält man
\(\seteqnumber{0}{}{68}\)\begin{equation*} h_\mathrm {sys} \approx \dfrac { \lambda _{\mathrm {A}}\lambda _{\mathrm {B}} \left ( T_{\mathrm {Test,A}}+T_{\mathrm {Test,B}} \right ) } { \lambda _{\mathrm {A}} T_{\mathrm {Test,B}} + \lambda _{\mathrm {B}} T_{\mathrm {Test,A}} + 2 } \end{equation*}
Unter der zusätzlichen Bedingung, dass die Testintervalle auch für die Ausfallrate des jeweils anderen Kanals ausreichend kurz wären, also \(\lambda _{\mathrm {A}} T_{\mathrm {Test,B}} \ll 1\) und \(\lambda _{\mathrm {B}} T_{\mathrm {Test,A}} \ll 1\) können die Produkte im Nenner vernachlässigt werden:
\(\seteqnumber{0}{}{68}\)\begin{equation*} h_\mathrm {sys} \approx \lambda _{\mathrm {A}} \lambda _{\mathrm {B}} \dfrac {T_{\mathrm {Test,A}} + T_{\mathrm {Test,B}}}{2} \end{equation*}
Dies ist die bereits für die Berechnung der Ausfallrate eines Minimalschnitts bekannte Formel (64), angewandt auf den einzigen Minimalschnitt dieses Markov-Modells {A&B}:
\(\seteqnumber{0}{}{68}\)\begin{equation*} h_\mathrm {sys} = h_\mathrm {MCS} \lessapprox \lambda _{\mathrm {A}} Q_{\mathrm {B}} + \lambda _{\mathrm {B}} Q_{\mathrm {A}} \lessapprox \lambda _{\mathrm {A}} \lambda _{\mathrm {B}} \dfrac {T_{\mathrm {Test,B}}}{2} + \lambda _{\mathrm {B}} \lambda _{\mathrm {A}} \dfrac {T_{\mathrm {Test,A}}}{2} = \lambda _{\mathrm {A}} \lambda _{\mathrm {B}} \dfrac {T_{\mathrm {Test,A}} + T_{\mathrm {Test,B}}}{2} \end{equation*}
6.3 Erwartungswert der Ausfälle
Für reparierbare bzw. ersetzbare Systeme ist neben der Ausfallrate noch der Erwartungswert der Ausfälle \(N(t)\) interessant:
\(\seteqnumber{0}{}{68}\)\begin{equation} N_\mathrm {sys}(T) = \int \limits _0^T h_\mathrm {sys}(t) dt \end{equation}
Er gibt an, wie viele Ausfälle im Zeitintervall \(t=0\dots T\) zu erwarten sind.
Die mittlere Ausfallrate \(\overline {h}\) kann auch aus \(N(T)\) berechnet werden:
\(\seteqnumber{0}{}{69}\)\begin{equation} \label {eq:h_mean_N} \overline {h_\mathrm {sys}} = \mathrm {PFH} = \frac {N_\mathrm {sys}(T)}{T} \end{equation}