Berechnungen zur Funktionalen Sicherheit
Größen, Formeln und Methoden

4 Wiederherstellung und Verfügbarkeit

Bei Komponenten und Systemen, die im Fall eines Ausfalls repariert oder ersetzt werden, sind weitere Betrachtungen und Größen erforderlich.

4.1 Reparierbarkeit

Wenn davon ausgegangen werden muss, dass es während der spezifizierten Einsatzdauer des Gesamtsystems zu mehreren Ausfällen der Funktion kommen kann, ist ein System (bzw. eine Funktion) reparierbar. Dabei spielt es keine Rolle, ob das System im wörtlichen Sinne repariert wird, oder einzelne Komponenten oder sogar das ganze System durch ein gleiches oder anderes ersetzt wird. Reparierbarkeit ist also keine Definitionssache (wie die Festlegung einer kleinsten tauschbaren Einheit oder des Totalschadens), sondern ergibt sich durch die Zuverlässigkeiten der Komponenten und die geplante Einsatzdauer zwangsläufig. Die viel einfachere Modellierung einer Funktion als nicht-reparierbar darf nur dann gewählt werden, wenn die Unzuverlässigkeit sämtlicher Komponenten über die angedachte, spezifizierte Einsatzdauer klein ist (etwa kleiner 0,1). Dies ist bei langlebigen Systemen wie Flugzeugen, Eisenbahnen, Maschinen oder Industrieanlagen praktisch nie erfüllt, bei kurzlebigen wie PKW nur bei manchen Funktionen.

4.2 Diagnose, Test, Wiederherstellung

Als Diagnose bezeichnet man gemäß [IEC 61508] und anderen Normen die Maßnahmen, die einen Fehler innerhalb der Prozessfehlertoleranzzeit (PFTZ, auch als Prozess-Sicherheitszeit bezeichnet) entdecken. Das ist die Zeit, die ein physikalischer Prozess (z. B. ein Motor oder ein Ventil in einer Maschine) falsch angesteuert werden darf, ohne dass hierdurch ein unkontrollierbarer oder gefährlicher Systemzustand resultiert.

Als Tests werden die Maßnahmen bezeichnet, die Fehler erst nach einer mehr oder weniger genau definierten Fehleroffenbarungszeit offenbaren, beispielsweise im Rahmen eines Neustarts (Power-on-Self-Test), einer regelmäßig durchzuführenden Testroutine (Prüflauf) oder bei einer Wartungsmaßnahme (Werkstattinspektion). Die mittlere Zeit, in der ein vorhandener Fehler detektiert wird, wird meist mit MTTD (engl. Mean Time To Detect) abgekürzt. Wird ein Test in regelmäßigen Abständen \(T_{\mathrm {test}}\) durchgeführt, so beträgt die \(\mathrm {MTTD}=T_{\mathrm {test}}/2\).

Im Fall eines erkannten Defekts wird entweder die defekte Komponente repariert oder ersetzt, oder ein ganzes Modul ersetzt oder gar das ganze System (Maschine, Fahrzeug,...) außer Betrieb genommen und durch ein neues ersetzt. In jedem Fall wird die Funktion wieder hergestellt, denn diese wird ja in der Regel weiterhin benötigt. Mit welcher Maßnahme die Funktion konkret wieder hergestellt wird, spielt für die weiteren Betrachtungen keine Rolle.

4.3 Verfügbarkeit und Nichtverfügbarkeit

Verfügbarkeit \(A(t)\) ist die Wahrscheinlichkeit, dass eine Komponente/ein System/eine Funktion zum Zeitpunkt \(t\) funktioniert.

Nichtverfügbarkeit \(Q(t)\) ist die Wahrscheinlichkeit, dass eine Komponente/ein System/eine Funktion zum Zeitpunkt \(t\) nicht funktioniert. Sie ist folglich die Gegenwahrscheinlichkeit zur Verfügbarkeit:

\begin{equation} A(t) = 1 - Q(t) \quad \textrm {bzw.} \quad Q(t) = 1 - A(t) \end{equation}

Die Verfügbarkeit ist die entscheidende Größe bei Systemen/Funktionen, die nur gelegentlich benötigt werden, insbesondere also Funktionen, die nur in Ausnahme- oder Notfällen benötigt werden (z. B. Alarme oder Löscheinrichtungen). Sie ist auch eine wesentliche Größe bei Systemen/Funktionen, die Redundanzen aufweisen, sogenannte mehrkanalige Systeme, hierzu später mehr.

Für eine Komponente oder ein System, welches nie getestet und somit auch nie repariert oder ersetzt wird, gilt:

\begin{equation} Q(t) = F(0,t) \end{equation}

Die Verfügbarkeit kann durch kontinuierliche Diagnose oder regelmäßige Tests und falls nötig Wiederherstellung maßgeblich erhöht werden. Dies ist der Grund, warum praktisch alle Notfallsysteme regelmäßig getestet werden.

Wenn eine Komponente getestet und im Fall eines Defekts repariert oder ausgetauscht wird, gilt \(Q(t) = F(t)\) nur bis zum ersten Test. Im Fall von regelmäßigen Tests im Abstand von \(T_{\mathrm {test}}\) gilt bis zur ersten Wiederherstellung theoretisch:

\begin{equation*} Q(t) = \frac { F(t - t \bmod T_{\mathrm {test}},t) } { R(0, t - t \bmod T_{\mathrm {test}}) } = \frac { F(t) - F(t - t \bmod T_{\mathrm {test}}) }{ R(t - t \bmod T_{\mathrm {test}}) } \end{equation*}

Da aber nicht bekannt ist, wann der erste Defekt auftritt und somit die erste Reparatur oder der erste Austausch erforderlich ist, ist diese Formel praktisch bedeutungslos. Aus demselben Grund ist auch eine veränderliche Ausfallrate praktisch bedeutungslos, denn man kann ja nie sagen, wie lange zum Zeitpunkt \(t\) eine Komponente bereits im Einsatz gewesen ist, da man nicht weiß, wann sie eingebaut wurde – es könnte sich ja bereits um einen Ersatz handeln. Folglich muss immer eine mittlere Ausfallrate \(\overline {h}=\lambda =1/\mathrm {MTTF}\) gemäß Abschnitt 3 bestimmt und verwendet werden.

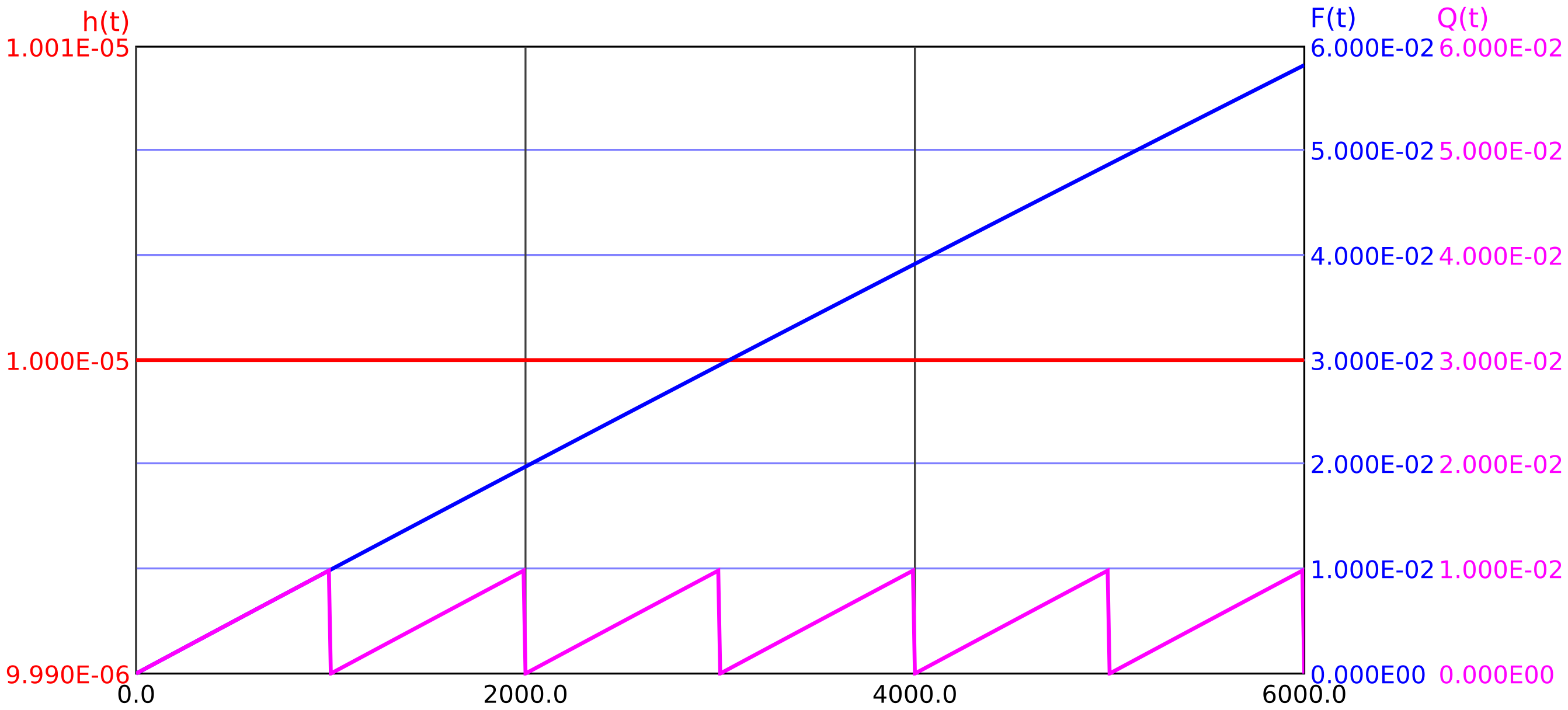
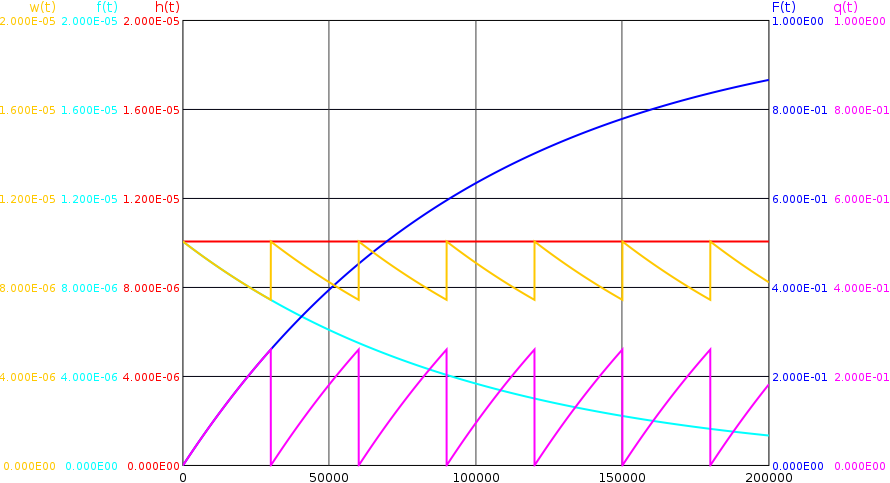
Die Nichtverfügbarkeit ist für Komponenten und Systeme, welche regelmäßig (und vollständig) getestet werden, daher eine periodische Aneinanderreihung von Anfangsstücken der Exponentialverteilung:

\begin{equation} Q(t) = F(0, t \bmod T_{\mathrm {test}}) = 1-\mathrm {e}^{-\lambda (t \bmod T_{\mathrm {test}} )} \label {eq:q_t_exakt} \end{equation}

Ist die Zeit \(t\) klein im Verhältnis zu \(\mathrm {MTTF}=1/\lambda \), so gilt geringfügig konservativ

\begin{equation} Q(t) \lessapprox \lambda \cdot (t \bmod T_{\mathrm {test}} ) \label {eq:q_t_approx} \end{equation}

Für eine mittlere Ausfallrate \(h(t)=\lambda =\SI {1e-5}{\per \hour }\) und ein Testintervall \(T_{\mathrm {test}}=\SI {1000}{\hour }\) sind Nichtverfügbarkeit \(Q(t)\) und Unzuverlässigkeit \(F(t)\) in Abbildung 9 dargestellt.

Die Nichtverfügbarkeit sinkt bei jedem Test auf null, um dann erneut anzusteigen. Dabei wird vorausgesetzt, dass der regelmäßige Test vollständig ist, also alle relevanten Fehler der Komponente offenbart. Ist dies nicht der Fall, muss dieser verbleibende Anteil als weitere Nichtverfügbarkeit mit einer entsprechend kleineren Ausfallrate, aber längeren Testzeit (dann meist die System-Lebenszeit) hinzugefügt werden. Überschlagsmäßig kann man diese zweite Nichtverfügbarkeit einfach addieren, in speziellen Software-Werkzeugen (FTA- oder Markov-Tools) ist auch eine exakte Behandlung möglich.

Beispiel 4.1 Ein Rauchmelder habe eine mittlere Ausfallrate von \(\overline {h(t)}=\lambda =1/\SI {100000}{\hour }=\SI {1e-5}{\per \hour }\). Er werde jährlich (alle \(T=\SI {8760}{\hour }\)) getestet und falls erforderlich ersetzt. Wie groß ist die Wahrscheinlichkeit, dass er im Fall eines Brandes nicht funktioniert?

Es muss die mittlere Nichtverfügbarkeit über das Testintervall \(T_\mathrm {test}\) bestimmt werden:
\(\seteqnumber{0}{}{40}\)
\begin{equation*} \overline {Q(0..T)} = \frac {1}{T} \int \limits _0^T{1 - \mathrm {e}^{-\lambda \cdot t}} dt = \frac {1}{T} \left ( t + \frac {1}{\lambda } \mathrm {e}^{-\lambda \cdot t} \right ) \Bigg |_0^T = 1 + \frac {\mathrm {e}^{-\lambda \cdot T} - 1}{\lambda \cdot T} = 0,0426 \end{equation*}

Wenn die Nichtverfügbarkeit klein ist (etwa \(Q<\num {0.1}\)), gilt sehr gut die konservative Näherung:

\begin{equation} \overline {Q(0..T_\mathrm {test})} \lessapprox \num {0.5}\cdot \lambda \cdot T_\mathrm {test} \label {eq:q_mean_approx} \end{equation}

Im vorherigen Beispiel ergäbe sich \(\overline {Q(0..T_\mathrm {test})} \approx \num {0.0438}\) statt 0,0426.

Die Nichtverfügbarkeit ist zwar wie die Unzuverlässigkeit eine Wahrscheinlichkeit, kann also nur Werte von 0 bis 1 annehmen, sie ist jedoch im Gegensatz zur Unzuverlässigkeit nur im Sonderfall eines nicht-testbaren Systems monoton steigend. Nach jedem Test hingegen fällt die Nichtverfügbarkeit \(Q(t)\) im Gegensatz zur Unzuverlässigkeit \(F(t)\) wieder auf null (bzw. im Fall eines nicht vollständigen Tests zumindest auf einen Wert nahe null).

4.4 Zeit zur Reparatur, MRT

Falls durch den Defekt nur eine Teilfunktion betroffen ist, der Weiterbetrieb des umgebenden größeren Systems aber (ggf. mit Einschränkungen) möglich ist, muss auch die für die Reparatur und/oder Ersatzbeschaffung benötigte Zeit (MRT, Mean Repair Time) in der Verfügbarkeit berücksichtigt werden. Zusammen mit der Zeit zur Entdeckung (MTTD) ergibt sich die mittlere Wiederherstellungszeit (Mean Time To Restore, MTTR):

\begin{equation} \mathrm {MTTR} = \mathrm {MTTD} + \mathrm {MRT} \end{equation}

Zur exakten Berechnung der mittleren Nichtverfügbarkeit kann man von deren Definition ausgehen:

\begin{align} \label {eq:mean_q_test_rep} \begin{split} \overline {Q} &= \frac {T_{\mathrm {defekt}}}{T_{\mathrm {gesamt}}} = \frac { T_{\mathrm {ud}} + p_{\mathrm {def}} \cdot \mathrm {MRT} } {(1-p_{\mathrm {def}}) \cdot T_{\mathrm {test}} + p_{\mathrm {def}} \cdot (T_{\mathrm {test}}+\mathrm {MRT} )} \\ &= \frac { T_{\mathrm {ud}} + p_{\mathrm {def}} \cdot \mathrm {MRT} } { T_{\mathrm {test}} + p_{\mathrm {def}} \cdot \mathrm {MRT} } \end {split} \end{align}

Dabei bezeichnet \(p_{\mathrm {def}}\) die Wahrscheinlichkeit, die Funktion zum regelmäßigen Testzeitpunkt \(T_{\mathrm {test}}\) als defekt vorzufinden

\[ p_{\mathrm {def}} = F(T_{\mathrm {test}}) = 1-e^{-\lambda \cdot T_{\mathrm {test}}} \]

und \(T_{\mathrm {ud}}\) die mittlere Zeit in jedem Testintervall, während der die Funktion aufgrund des Defekts unerkannt nicht verfügbar ist (also quasi die MTTD aufgeteilt auf alle Testintervalle bis zum Ausfall)

\[ \begin {split} T_{\mathrm {ud}} &= \int \limits _0^{T_{\mathrm {test}}} f(t) \cdot (T_{\mathrm {test}} - t)\;dt = \int \limits _0^{T_{\mathrm {test}}} \lambda \cdot e^{-\lambda \cdot T_{\mathrm {test}} } \cdot (T_{\mathrm {test}} - t) \;dt\\ &= \frac {e^{-\lambda \cdot T_{\mathrm {test}}} -1} {\lambda } +T_{\mathrm {test}} \end {split} \]

Durch Einsetzen in Formel (43) ergibt sich für die mittlere Nichtverfügbarkeit

\begin{align} \label {eq:q_mean_exact_mttr} \begin{split} \overline {Q} &= \frac { \dfrac {e^{-\lambda \cdot T_{\mathrm {test}}}-1}{\lambda } + T_{\mathrm {test}} + \mathrm {MRT} \cdot ( 1-e^{-\lambda \cdot T_{\mathrm {test}}} ) } { T_{\mathrm {test}} + \mathrm {MRT} \cdot ( 1-e^{-\lambda \cdot T_{\mathrm {test}}} ) } \\ &= \frac { e^{-\lambda \cdot T_{\mathrm {test}}} - 1 } { \lambda \cdot T_{\mathrm {test}} + \lambda \cdot \mathrm {MRT} \cdot ( 1-e^{-\lambda \cdot T_{\mathrm {test}}} ) } + 1 \end {split} \end{align}

Für vernachlässigbare Detektionszeit \(T_{\mathrm {test}} \rightarrow 0\) (kontinuierliche Diagnose, kleine Testintervalle oder Fehleroffenbarung durch unmittelbar erkennbare Fehlfunktion) geht die mittlere Nichtverfügbarkeit gegen

\begin{equation} \label {eq:q_mean_MRT} \overline {Q} = \frac { \lambda \cdot \mathrm {MRT} } { \lambda \cdot \mathrm {MRT} + 1 } \end{equation}

wie man durch einmalige Anwendung der Regel von de l’Hospital auf Formel (44) erhält.

Für vernachlässigbare Reparaturzeit \(\mathrm {MRT} \rightarrow 0\) (z. B. Außerbetriebnahme während der Reparatur) vereinfacht sich Formel (44) unmittelbar zu

\begin{equation} \label {eq:q_mean_test} \overline {Q} = \frac {e^{-\lambda \cdot T_{\mathrm {test}}}-1} {\lambda \cdot T_{\mathrm {test}} }+1 \end{equation}

Wenn sowohl Testintervall \(T_{\mathrm {test}}\) als auch Reparaturzeit \(\mathrm {MRT}\) klein gegen \(MTTF\) sind, gilt mit ausreichender Genauigkeit

\begin{equation} \label {eq:q_mean_approx_mttr} \overline Q \lessapprox \lambda \cdot \left ( \num {0,5}\cdot T_{\mathrm {test}} + \mathrm {MRT} \right ) \end{equation}

Schwieriger ist die Herleitung einer (exakten) Formel für die Nichtverfügbarkeit zu einem bestimmten Zeitpunkt, wenn die Reparaturzeit nicht vernachlässigbar klein ist. Eine sehr gute Näherung ist durch

\begin{equation} \label {eq:q_t_mttr} Q(t) = 1-\frac { e^{-\;\dfrac {\lambda \cdot (t \bmod T_{\mathrm {test}}) }{ \lambda \cdot \mathrm {MRT} + 1 }} }{ \lambda \cdot \mathrm {MRT} + 1 } \end{equation}

gegeben (ohne Herleitung). Für Reparaturzeit \(\mathrm {MRT} \rightarrow 0\) geht Formel (48) unmittelbar in Formel (39) über:

\[ Q(t) = 1-\mathrm {e}^{-\lambda (t \bmod T_{\mathrm {test}} )} \]

Für vernächlässigbare Detektionszeit \(T_{\mathrm {test}} \rightarrow 0\) ergibt sich unmittelbar

\[ Q(t) = 1-\frac { e^{-\;\dfrac {0}{ \lambda \cdot \mathrm {MRT} + 1 }} }{ \lambda \cdot \mathrm {MRT} + 1 } = 1-\frac {1}{ \lambda \cdot \mathrm {MRT} + 1 } = \frac { \lambda \cdot \mathrm {MRT} } { \lambda \cdot \mathrm {MRT} + 1 } = \overline {Q} \]

also Formel (45).

4.5 Kontinuierliche Diagnose

Im Fall von kontinuierlicher vollständiger Diagnose (d. h. jeder Fehler wird sofort entdeckt) hat die Nichtverfügbarkeit gar nichts mit der (Un-)zuverlässigkeit zu tun, es gilt also immer \(Q(t) \neq F(t)\). Die Nichtverfügbarkeit ist dann nur von der (mittleren) Ausfallrate \(\overline {h}=\lambda \) und der für die Wiederherstellung nötigen Zeit \(\mathrm {MRT}\) abhängig:

\begin{equation} \label {eq:q_MRT} Q(t) = \overline {Q} = \frac { \lambda \cdot \mathrm {MRT} } { \lambda \cdot \mathrm {MRT} + 1 } = \mathrm {const} \end{equation}

Wird die Komponente nie getestet und ggf. repariert oder ersetzt, so ist \(Q(t)=F(t)\). Dies mag in der (unbemannten) Raumfahrt der Fall sein, in der funktionalen Sicherheit jedoch nicht, da das regelmäßige Testen und ggf. Reparieren oder Ersetzen zentrale Maßnahmen der funktionalen Sicherheit darstellen. Daher dürfen Unzuverlässigkeit und Nichtverfügbarkeit niemals verwechselt werden. Des Weiteren darf niemals eine Unzuverlässigkeit und eine Nichtverfügbarkeit addiert oder multipliziert oder sonst mathematisch verknüpft werden!

Beispiel 4.2 Eine Komponente mit der konstanten Ausfallrate \(h(t)=\lambda =1/\SI {10000}{\hour }=\SI {1e-4}{\per \hour }\) werde alle 5000 Stunden getestet und erforderlichenfalls umgehend repariert oder ausgetauscht. Wie hoch sind Nichtverfügbarkeit und Unzuverlässigkeit zu den Zeitpunkten T=19999 und T=20001 Stunden?
\(\seteqnumber{0}{}{49}\)
\begin{align*} Q(19999\,\mathrm {h}) &= 1 - \mathrm {e}^{-\lambda \cdot (19999-15000\,\mathrm {h})} \approx \num {0.3935} \\ Q(20001\,\mathrm {h}) &= 1 - \mathrm {e}^{-\lambda \cdot (20001-20000\,\mathrm {h})} \approx \num {0.0001} \\ F(19999\,\mathrm {h}) &= 1 - \mathrm {e}^{-\lambda \cdot 19999\,\mathrm {h}} \approx \num {0.8646} \\ F(20001\,\mathrm {h}) &= 1 - \mathrm {e}^{-\lambda \cdot 20001\,\mathrm {h}} \approx \num {0.8647} \end{align*}

4.6 Betriebliche und sicherheitsbezogene Verfügbarkeit

Häufig hört man als Sicherheitsingenieur den Satz: „Der Ausfall ist unkritisch, der geht nur in die Verfügbarkeit.“ Dieser Satz basiert auf dem Unverständnis von Zuverlässigkeit und Verfügbarkeit. Beides können sicherheitsbezogene Größen sein, müssen aber nicht.

Beispiel 4.3 Die Verfügbarkeit eines Rauchmelders gibt an, mit welcher Wahrscheinlichkeit er eine Rauchentwicklung melden wird. Dies ist offensichtlich eine sicherheitsrelevante Größe, in vielen Anwendungen gibt es daher vorgeschriebene Mindestwerte (bzw. Maximalwerte für die Nichtverfügbarkeit). Je häufiger man ihn testet, umso größer wird die Verfügbarkeit. Je größer die Ausfallrate, um so häufiger muss man testen (und reparieren), um die geforderte Verfügbarkeit zu erreichen. Die Zuverlässigkeit (oder Ausfallrate) alleine erlaubt hier keine Aussage über die Sicherheit, da es für die Gebäudesicherheit unrelevant ist, wie oft der Rauchmelder kaputt geht – wenn der Fehler nur schnell detektiert und behoben wird. Vielmehr ist die Zuverlässigkeit hier eine betrieblich relevante Größe: Je schlechter die Zuverlässigkeit (also je größer die Ausfallrate) des Rauchmelders, desto häufiger muss man ihn testen und ersetzen, um die aus Sicherheitsgründen vorgegebene Verfügbarkeit zu erreichen.

4.7 Ausfallrate bei Tests

Aufgrund der Tests und ggf. Reparatur verliert die Dichtefunktion \(f(t)\) ihre Bedeutung. An ihre Stelle tritt eine neue Größe, die meist als „Ausfallhäufigkeit“ bezeichnet wird. In [NUREG] wird für diese das Formelzeichen \(w(t)\) verwendet, jedoch hat sich auch für diese Größe noch kein einheitliches Formelzeichen durchgesetzt. In Abbildung 10 sind alle drei Größen \(h(t)\), \(w(t)\) und \(f(t)\) für eine Funktion mit der konstanten Ausfallrate \(h(t)=\lambda =\SI {1e-5}{\per \hour }\), die alle 30000 Stunden getestet wird, dargestellt.

Im Gegensatz zur Dichte \(f(t)\) wird \(w(t)\) niemals null, da sich aufgrund der Reparatur das System ja immer (wieder) in einem Zustand befindet, in dem es (wieder) ausfallen kann. Unmittelbar nach (vollständigen) Tests, also wenn die Nichtverfügbarkeit auf null zurückgeht, steigt die Ausfallhäufigkeit wieder auf die Ausfallrate \(h(t)\) an. Das Integral der Ausfallhäufigkeit \(w(t)\) über die Zeit kann also beliebig groß werden. Nur bis zum ersten Ausfall bzw. dem ersten Test sind \(w(t)\) und \(f(t)\) identisch.

Die Ausfallrate, also die Häufigkeit des Übergangs in den Ausfallzustand unter der Bedingung, dass das System zum Zeitpunkt \(t\) ausfallfähig ist, berechnet sich nun zu

\begin{equation} h(t) = \frac {w(t)}{A(t)} = \frac {w(t)}{1-Q(t)} \end{equation}

wobei \(A(t)\) die Verfügbarkeit bzw. \(Q(t)\) die Nichtverfügbarkeit zum Zeitpunkt \(t\) bezeichnet.

Berechnungen zur Funktionalen Sicherheit Größen, Formeln und Methoden